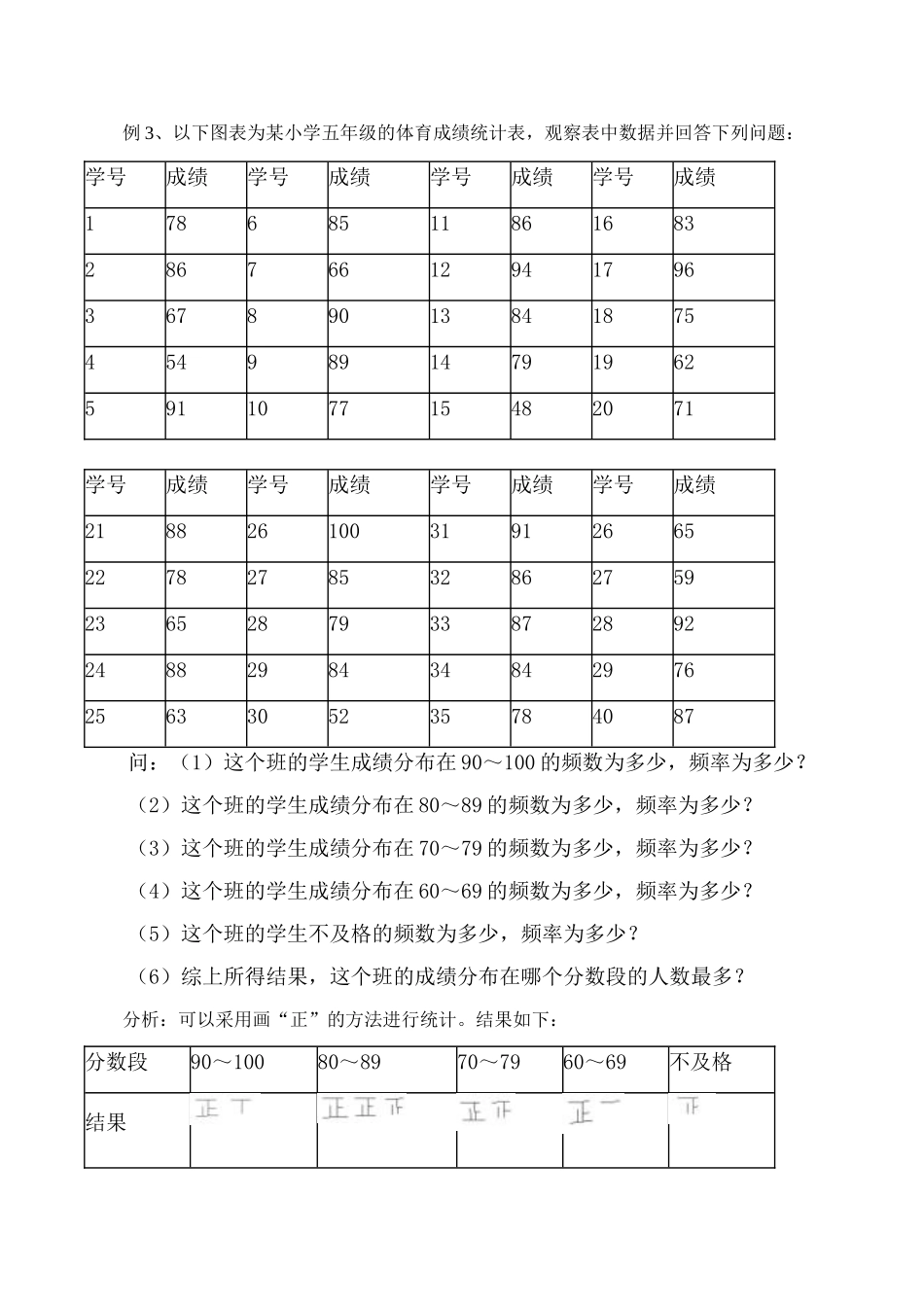
数据的收集学案知识要点:1.数据收集的过程:明确调查问题,确定调查对象,选择调查方法,展开调查,记录结果(一般以表格形式),得出结论。2.在一次实验统计中,某个对象出现的次数称为它的频数;这个次数与总次数的比值(或百分比),称为它出现的频率。频数和频率能反映出该对象出现的频繁程度。3.随着实验次数增加,频数也会跟着增加,但频率始终在0和1之间。例题解析:例1、建国以来,我国已经进行了五次人口普查,下表是历次普查得到的全国人口数量统计表:普查年份19531964198219902000人口数(亿)5.946.9510.0811.3412.95请问:(1)1953年我国人口数量是______亿,2000年我国人口数量是______亿;(2)从1953年至2000年,我国人口数量增加了______亿。解:(1)5.94,12.95;(2)7.01。例2、下面是几次投掷硬币的试验结果,仔细观察并回答下列问题:(1)第一次试验中,正面朝上的频数为______,反面朝上的频率为______。(2)第二次试验中,反面朝上的频数为______,出现正面的频率为______。(3)第三次试验中,正面朝上的频率为______,反面朝上的频率为______,两种频率的和为______。(4)第四次试验中,正面朝上的频率为______,反面朝上的频率为______,两种频率的和为______。(5)四次试验中抛掷硬币的总次数为______,出现反面朝上的总次数为______。分析:注意频数表示该对象出现的次数,而频数则表示频数与总数的比。解:(1)正面朝上的频数为14,反面朝上的频率为=。(2)反面朝上的频数为20,出现正面的频率为。(3)正面朝上的频率为=,反面朝上的频率为=,两种频率的和为。(4)正面朝上的频率为,反面朝上的频率为,两种频率的和为。(5)四次试验中抛掷硬币的总次数为30+40+50+60=180,出现反面朝上的总次数为16+20+24+31=91。例3、以下图表为某小学五年级的体育成绩统计表,观察表中数据并回答下列问题:学号成绩学号成绩学号成绩学号成绩17868511861683286766129417963678901384187545498914791962591107715482071学号成绩学号成绩学号成绩学号成绩218826100319126652278278532862759236528793387289224882984348429762563305235784087问:(1)这个班的学生成绩分布在90~100的频数为多少,频率为多少?(2)这个班的学生成绩分布在80~89的频数为多少,频率为多少?(3)这个班的学生成绩分布在70~79的频数为多少,频率为多少?(4)这个班的学生成绩分布在60~69的频数为多少,频率为多少?(5)这个班的学生不及格的频数为多少,频率为多少?(6)综上所得结果,这个班的成绩分布在哪个分数段的人数最多?分析:可以采用画“正”的方法进行统计。结果如下:分数段90~10080~8970~7960~69不及格结果解:(1)这个班的学生成绩分布在90~100的频数为7,频率为;(2)这个班的学生成绩分布在80~89的频数为14,频率为;(3)这个班的学生成绩分布在70~79的频数为9,频率为;(4)这个班的学生成绩分布在60~69的频数为6,频率为;(5)这个班的学生不及格的频数为4,频率为;(6)观察在这五个频数中14最大,而相应的频率也是最大的频率,所以这个班的成绩分布在80~89分数段的人数最多。例4、下面是某工厂工人的生日情况统计方格图,试回答下列问题:图5-1问:生日分布在1~3月份的频数为多少?4~6月份的呢?7~9月份的呢?10~12月份的呢?它们的频率又分别为几?分析:看条形图,首先要注意各个长方形分别代表哪一项,要求某时间段内的频数,只要把相应的长方形的数据相加即可。解:生日分布在1~3月份的频数为:2500+1100+3300=6900生日分布在4~6月份的频数为:5300+2200+1500=9000生日分布在7~9月份的频数为:4500+3500+1200=9200生日分布在10~12月份的频数为:2100+3600+2200=7900总数为:6900+9000+9200+7900=33000故各自的频率为:1~3月份为:6900÷33000=20.91%4~6月份为:9000÷33000=27.27%7~9月份为:9200÷33000=27.88%10~12月份为:7900÷33000=23.94%练习:1.请设计一张关于全班同学早上起床时间的统计表,将其分成5:30之前,5:30~5:59,6:00~6:29,6:30~6:59,7:00之后,这五个时间段,看看落在哪个时间段...