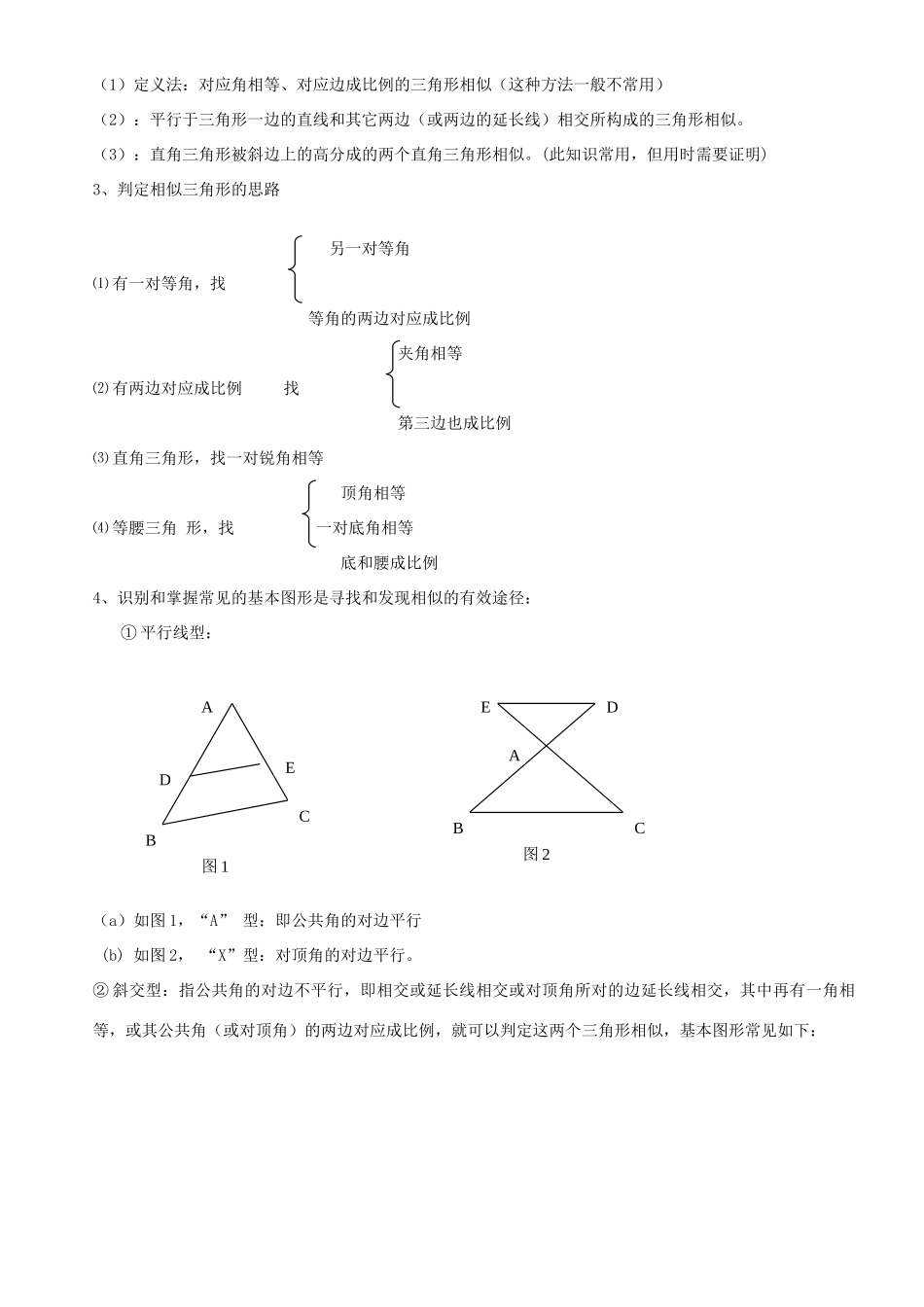
相似三角形判定方法探讨一、教学目标1、知识与技能熟练掌握相似三角形的判定方法,能灵活运用这些方法解决有关问题。探寻证明三角形相似的一般规律.2、过程与方法:通过对相似三角形判定方法的复习,能灵活解决相关问题。3、情感态度与价值观:充分运用观察、归纳、推理等手段,感受数学学习中的合情推理的说服力,积极参与推理活动,培养推理能力,激发对数学的兴趣。二、教学重点、难点重点:熟练掌握相似三角形的判定方法。难点:灵活运用判定方法解决实际问题。三、考点分析:1、相似三角形的判定及其应用。2、图形的相似在综合题中的应用。四、试题特点:三角形的相似在中考中主要有:填空、选择以及阅读理解题、探究性试题等题型。也有可能出现在综合题和压轴题中,题量约占总题量的6﹪。五、命题趋势:三角形相似是中考的重要内容,它的题型新颖,形式多样,常常与平行线、平行四边形、圆等知识结合起来考查,也有可能和二次函数结合起来考查,题型也增加了阅读理解题、开放性试题、探究性试题等新的题型。在复习中应注意对这部分知识的综合运用能力的培养和提高。六、教学过程学生回忆并整理:1、相似三角形的定义:对应角相等、对应边成比例的三角形叫做相似三角形。相似的符号为“~”。2、相似三角形的判定方法:判定方法(1)如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似。判定方法(2):如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。判定方法(3):如果一个三角形的三条边分别与另一个三角形的三条边对应成比例那么这两个三角形相似。除了上述三种判定方法外,还有以下三种判定方法:(1)定义法:对应角相等、对应边成比例的三角形相似(这种方法一般不常用)(2):平行于三角形一边的直线和其它两边(或两边的延长线)相交所构成的三角形相似。(3):直角三角形被斜边上的高分成的两个直角三角形相似。(此知识常用,但用时需要证明)3、判定相似三角形的思路另一对等角⑴有一对等角,找等角的两边对应成比例夹角相等⑵有两边对应成比例找第三边也成比例⑶直角三角形,找一对锐角相等顶角相等⑷等腰三角形,找一对底角相等底和腰成比例4、识别和掌握常见的基本图形是寻找和发现相似的有效途径:①平行线型:(a)如图1,“A”型:即公共角的对边平行(b)如图2,“X”型:对顶角的对边平行。②斜交型:指公共角的对边不平行,即相交或延长线相交或对顶角所对的边延长线相交,其中再有一角相等,或其公共角(或对顶角)的两边对应成比例,就可以判定这两个三角形相似,基本图形常见如下:ADEBCEDABC图1图2(a)如图3,若∠B=∠D或∠ACB=∠AED则△ABC~△ADE;(b)如图4,若∠ACD=∠B或∠ADC=∠ACB则△ACD~△ABC;(C)如图5,若∠ADE=∠B或∠AED=∠C则△ADE~△ABC;(d)如图6,若∠A=∠D或∠B=∠C,则△AOB~△DOC。③旋转型5、相似三角形判定定理的作用①可以用来判定两个三角形相似.②间接证明角相等或线段成比例.③间接地为计算线段的长度及角的大小创造条件.④三角形全等是三角形相似的特殊情形6应用举例(1)、满足下列条件,△ABC与△A′B′C′是否相似?说明理由。∠A=40º,∠B=80º,∠A′=80º∠B′=60º;解:相似。 ∠B=80º,∠A′=80º∴∠B=∠A′ ∠C=180º-∠A-∠B=180º-40º-80º=60ºA(D)BCEF图7旋转型的特点就是将其中一个图形旋转一定的角度,就可以得到平行线型或相交线型。AEBCD图3ADBC图4ADBC图5ABDC图6E又 ∠B′=60º∴∠C=∠B′∴△ABC和△A′B′C′(两角对应相等,两个三角形相似)点评:找准对应角相等。(2)、如图在平行四边形ABCD中,G是BC延长线上一点AG与BD交于点E,与DC交于点F,则图中相似•三角形共有()对•A3对BB4对C5对D6对解:如图 四边形ABCD是平行四边形,∴AD∥BCAB∥CD∴△FCG∽△ABG∽△FDA(3对),△AED∽△GEB(1对)△AEB∽△FED(1对),△ABD∽△CDB(1对),即有6对,∴选D点评:主要运用平行线知识判定三角形相似.。(3)、P是ΔABC中AB边上一点,过点P作直线(不与直线AB重合)截ΔABC,使截得...