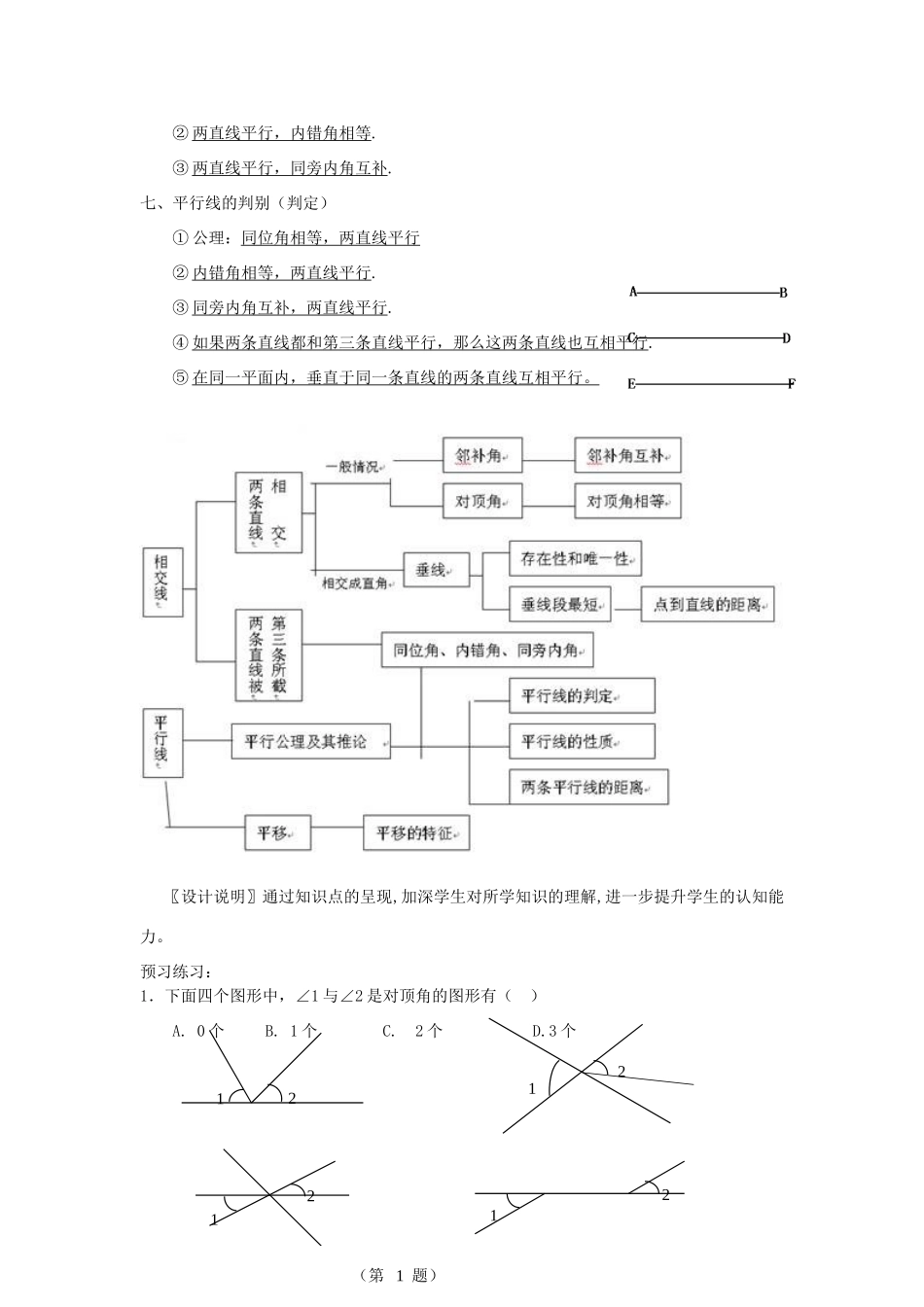
课案(教师用)相交线与平行线(复习课)【理论支持】数学教育家弗赖登塔尔认为,数学来源于现实,存在于现实,并且应用于现实,而且每个学生有各自不同的“数学现实”。数学教师的任务之一是帮助学生构造数学现实,并在此基础上发展他们的数学现实。因此,在教学过程中,教师应该充分利用学生的认知规律,及已有的生活经验和数学的实际。教学时,把那些最能反映现代生产、现代社会生活需要的最基本、最核心的数学知识和技能作为数学教育的内容.数学教育的内容不能仅仅局限于数学内部的内在联系,还应该研究数学与现实世界各种不同领域的外部关系和联系这样才能使学生一方面获得既丰富多彩而又错综复杂的“现实的数学”内容,掌握比较完整的数学体系.另一方面,学生也有可能把学到的数学知识应用于现实世界中去。数学教育应该为所有的人服务,应该满足全社会各种领域的不同层次的人对数学的不同水平的需求。除了要研究平面内两条直线间的位置关系(重点是垂直和平行关系),还包括平移变换的内容以及一些命题的内容,由于教学时间有限,为了使学生集中精力掌握最基础的知识,并形成一定的能力,教学时应注意突出重点.例如,研究两条直线的位置关系时,重点是要研究一些图形的性质,如对顶角相等、垂线的性质,以及平行线的判定和性质等,对于一些定义,不要作严格的形式化的要求.教科书中邻补角、对顶角的概念都是结合图形,分析其位置关系给出的;垂直、平行的概念则是承接了前面学段学过的概念.对于同位角、内错角、同旁内角的内容,教科书是在研究两条直线相交的基础上,进一步研究三条直线相交的角度引入的,主要是为接下来研究平行做准备。这里要求学生掌握基本概念即可,不要做过多的变式训练。再如,对于命题、定理、证明等概念,教科书是分阶段、分散安排的.在本章,要求学生在学过一些命题(包括数与代数的以及空间与图形的)的基础上,了解命题的概念以及命题的构成(如果……那么……的形式),知道命题的真假了解定理的概念等.【教学目标】知识技能回顾相交线和平行线的相关知识及平移的知识,并运用它们解决问题。数学思考丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维。解决问题通过观察、归纳、对比来寻找图形的位置和数量关系,从而发现图形的性质。情感态度在观察、操作、想象、说理、交流的过程中,发展空间观念,初步形成积极参与数学活动,与他人合作交流的意识,激发学习空间与图形的兴趣。【教学重难点】重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.难点:垂直、平行的性质和判定的综合应用.【课时安排】一课时【教学设计】课前延伸知识梳理:一、垂线的定义两条直线相交所成的四个角中,有一个角是直角,那么其他三个角也是直角,这时就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足。二、垂线的性质①经过直线外一点有且只有一条直线与已知直线垂直.②垂线段最短.三、点到直线的距离从直线外一点向已知直线作垂线,这一点和垂足之间线段的长度叫做点到直线的距离.四、两线四角形成的相关角①对顶角②邻补角五、三线八角形成的相关角①同位角②内错角③同旁内角六、平行线的性质(特征)①公理:两直线平行,同位角相等.②两直线平行,内错角相等.③两直线平行,同旁内角互补.七、平行线的判别(判定)①公理:同位角相等,两直线平行②内错角相等,两直线平行.③同旁内角互补,两直线平行.④如果两条直线都和第三条直线平行,那么这两条直线也互相平行.⑤在同一平面内,垂直于同一条直线的两条直线互相平行。〖设计说明〗通过知识点的呈现,加深学生对所学知识的理解,进一步提升学生的认知能力。预习练习:1.下面四个图形中,∠1与∠2是对顶角的图形有()A.0个B.1个C.2个D.3个21122112(第1题)〖设计说明〗本题考查学生对对顶角概念的理解,加深学生对平面图形的认识和理解。2.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是()A.第一次右拐50°,第二次左拐130°,B.第一次左拐50°,第二次右拐50°,C.第一次左...