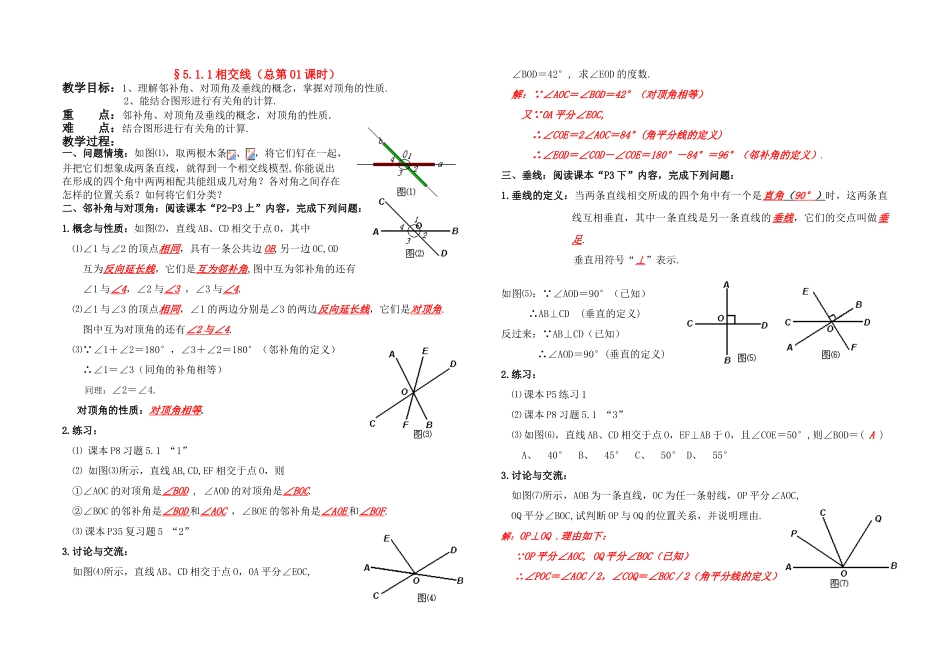
§5.1.1相交线(总第01课时)教学目标:1、理解邻补角、对顶角及垂线的概念,掌握对顶角的性质.2、能结合图形进行有关角的计算.重点:邻补角、对顶角及垂线的概念,对顶角的性质.难点:结合图形进行有关角的计算.教学过程:一、问题情境:如图⑴,取两根木条、,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线模型,你能说出在形成的四个角中两两相配共能组成几对角?各对角之间存在怎样的位置关系?如何将它们分类?二、邻补角与对顶角:阅读课本“P2-P3上”内容,完成下列问题:1.概念与性质:如图⑵,直线AB、CD相交于点O,其中⑴∠1与∠2的顶点相同,具有一条公共边OB,另一边OC,OD互为反向延长线,它们是互为邻补角,图中互为邻补角的还有∠1与∠4,∠2与∠3,∠3与∠4.⑵∠1与∠3的顶点相同,∠1的两边分别是∠3的两边反向延长线,它们是对顶角.图中互为对顶角的还有∠2与∠4.⑶ ∠1+∠2=180°,∠3+∠2=180°(邻补角的定义)∴∠1=∠3(同角的补角相等)同理:∠2=∠4.对顶角的性质:对顶角相等.2.练习:⑴课本P8习题5.1“1”⑵如图⑶所示,直线AB,CD,EF相交于点O,则①∠AOC的对顶角是∠BOD,∠AOD的对顶角是∠BOC.②∠BOC的邻补角是∠BOD和∠AOC,∠BOE的邻补角是∠AOE和∠BOF.⑶课本P35复习题5“2”3.讨论与交流:如图⑷所示,直线AB、CD相交于点O,OA平分∠EOC,∠BOD=42°,求∠EOD的度数.解: ∠AOC=∠BOD=42°(对顶角相等)又 OA平分∠EOC,∴∠COE=2∠AOC=84°(角平分线的定义)∴∠EOD=∠COD-∠COE=180°-84°=96°(邻补角的定义).三、垂线:阅读课本“P3下”内容,完成下列问题:1.垂线的定义:当两条直线相交所成的四个角中有一个是直角(90°)时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,它们的交点叫做垂足.垂直用符号“⊥”表示.如图⑸: ∠AOD=90°(已知)∴AB⊥CD(垂直的定义)反过来: AB⊥CD(已知)∴∠AOD=90°(垂直的定义)2.练习:⑴课本P5练习1⑵课本P8习题5.1“3”⑶如图⑹,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD=(A)A、40°B、45°C、50°D、55°3.讨论与交流:如图⑺所示,AOB为一条直线,OC为任一条射线,OP平分∠AOC,OQ平分∠BOC,试判断OP与OQ的位置关系,并说明理由.解:OP⊥OQ.理由如下: OP平分∠AOC,OQ平分∠BOC(已知)∴∠POC=∠AOC/2,∠COQ=∠BOC/2(角平分线的定义)又 ∠AOC+∠BOC=180°(邻补角的性质)∴∠POC+∠COQ=∠AOC/2+∠BOC/2=(∠AOC+∠BOC)/2=90°∴OP⊥OQ(垂直的定义).四、课堂小结:邻补角(邻补角互补)两条直线相交特例垂直对顶角(对顶角相等)五、课堂检测:⒈下列说法正确的是(D)A、相等的两个角是对顶角B、有公共顶点且相等的两个角是对顶角C、两条直线相交,构成的角是对顶角D、角的两边互为反向延长线的两个角是对顶角⒉若一对邻补角的差是60°,则这两个角分别是(B)A、100°,140°B、110°,70°C、160°,200°D、25°,65°⒊如图⑻,直线AB、CD相交于点O,若∠AOC=34°,∠DOE=56°,则∠BOD=34°,∠BOC=146°,∠AOE=90°.⒋如图⑼,OA⊥OB,∠1=∠2,求∠COD的度数.解: OA⊥OB(已知)∴∠AOB=90°(垂直的定义)即∠2+∠BOC=90°又 ∠1=∠2(已知)∴∠1+∠BOC=90°(等量代换)∴∠COD=90°六、课后作业:⒈书面作业:⒈课本P8习题5.1“2”如图⑽,直线AB,CD,EF相交于点O,⑴写出∠AOC,∠BOE的邻补角;⑵写出∠DOA,∠EOC的对顶角;⑶如果∠AOC=50°,求∠BOD,∠COB的度数.解:⑴∠AOC的邻补角分别是:∠AOD,∠COB;∠BOE的邻补角分别是:∠AOE,∠FOB.⑵∠DOA的对顶角是∠COB;∠EOC的对顶角∠DOF.⑶ ∠AOC=50°(已知)∴∠BOD=∠AOC=50°(对顶角相等)又 ∠AOC+∠COB=180°(邻补角互补)∴50°+∠COB=180°(等量代换)∴∠COB=130°(等式的性质)⒉课本P8习题5.1“7”如图⑾,直线AB,CD,相交于点O,∠EOC=70°,OA平分,求∠BOD的度数.解: OA平分∠EOC(已知)∴∠AOC=∠EOC/2(角平分线的定义)又 ∠EOC=70°(已知)∴∠AOC=35°又 ∠BOD=∠AOC(对顶角相等)∴∠BOD=35...