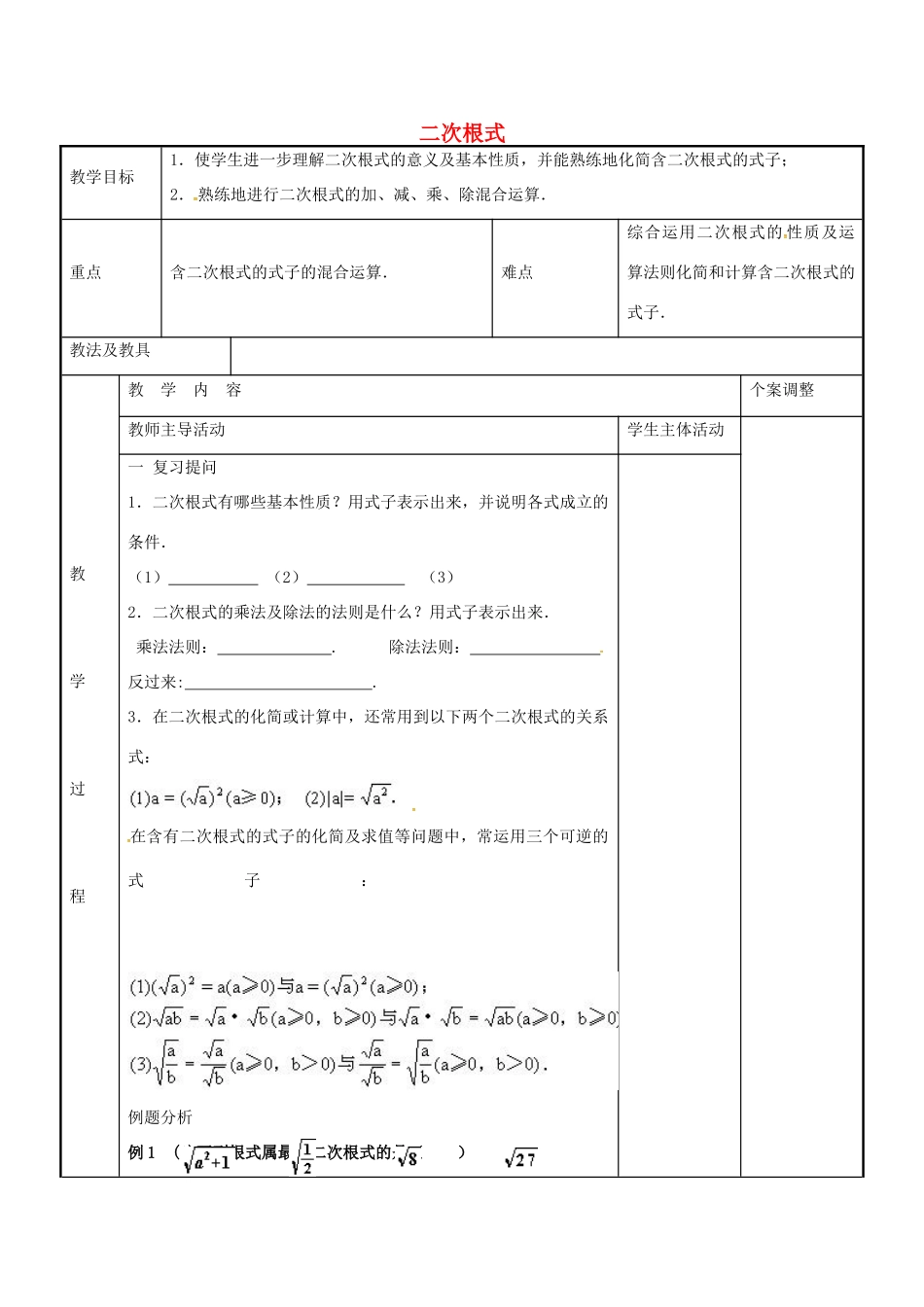
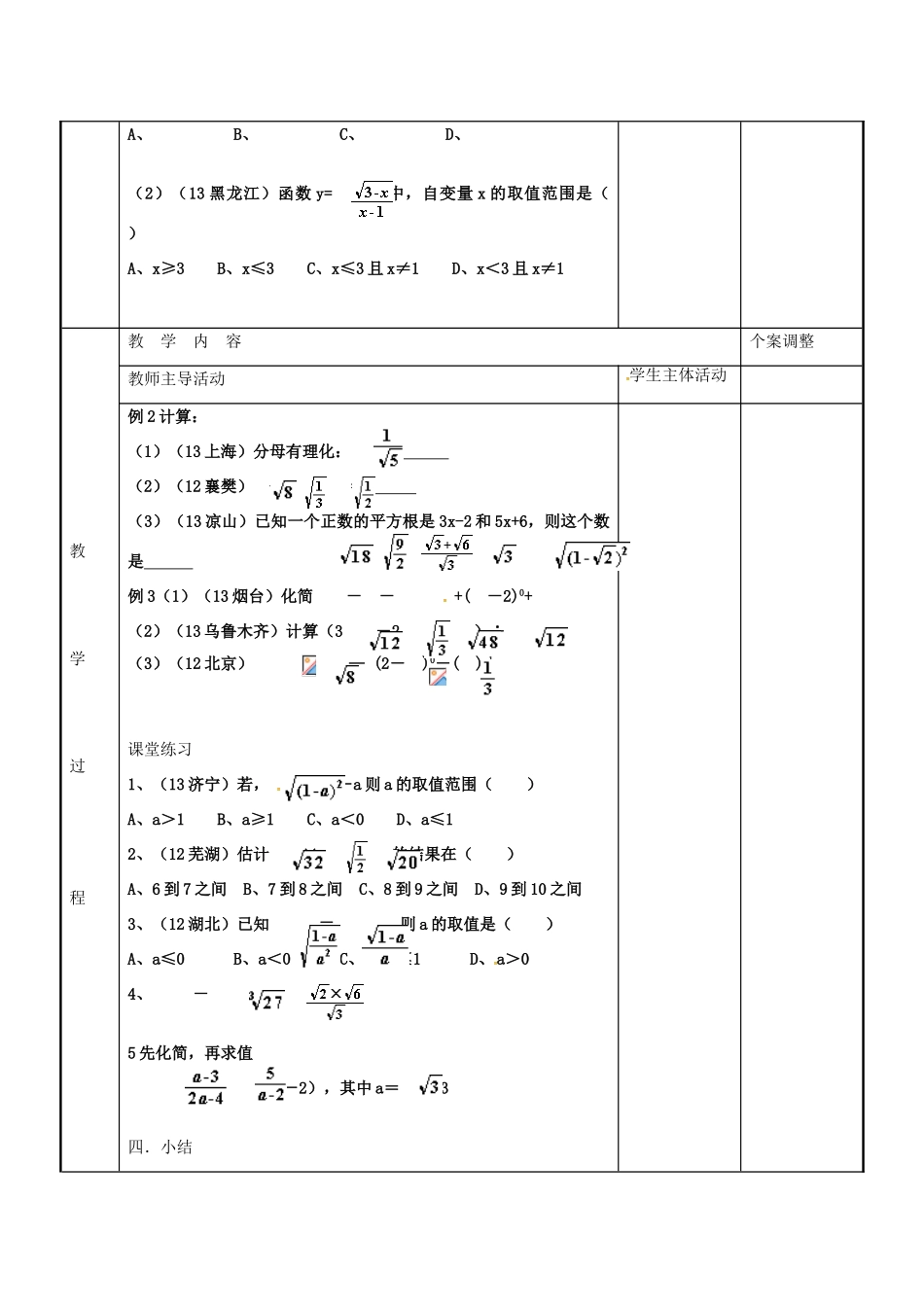
二次根式教学目标1.使学生进一步理解二次根式的意义及基本性质,并能熟练地化简含二次根式的式子;2.熟练地进行二次根式的加、减、乘、除混合运算.重点含二次根式的式子的混合运算.难点综合运用二次根式的性质及运算法则化简和计算含二次根式的式子.教法及教具教学过程教学内容个案调整教师主导活动学生主体活动一复习提问1.二次根式有哪些基本性质?用式子表示出来,并说明各式成立的条件.(1)(2)(3)2.二次根式的乘法及除法的法则是什么?用式子表示出来.乘法法则:.除法法则:反过来:.3.在二次根式的化简或计算中,还常用到以下两个二次根式的关系式:在含有二次根式的式子的化简及求值等问题中,常运用三个可逆的式子:例题分析例1(1)下列根式属最简二次根式的是()A、B、C、D、(2)(13黑龙江)函数y=中,自变量x的取值范围是()A、x≥3B、x≤3C、x≤3且x≠1D、x<3且x≠1教学过程教学内容个案调整教师主导活动学生主体活动例2计算:(1)(13上海)分母有理化:=(2)(12襄樊)+-2=(3)(13凉山)已知一个正数的平方根是3x-2和5x+6,则这个数是例3(1)(13烟台)化简--+(-2)0+(2)(13乌鲁木齐)计算(3-2+)÷(3)(12北京)—(2-)0-()-1课堂练习1、(13济宁)若,=1-a则a的取值范围()A、a>1B、a≥1C、a<0D、a≤12、(12芜湖)估计×+的结果在()A、6到7之间B、7到8之间C、8到9之间D、9到10之间3、(12湖北)已知=,则a的取值是()A、a≤0B、a<0C、0<a≤1D、a>04、-5先化简,再求值÷(-a-2),其中a=-3四.小结板书设计(用案人完成)教学札记