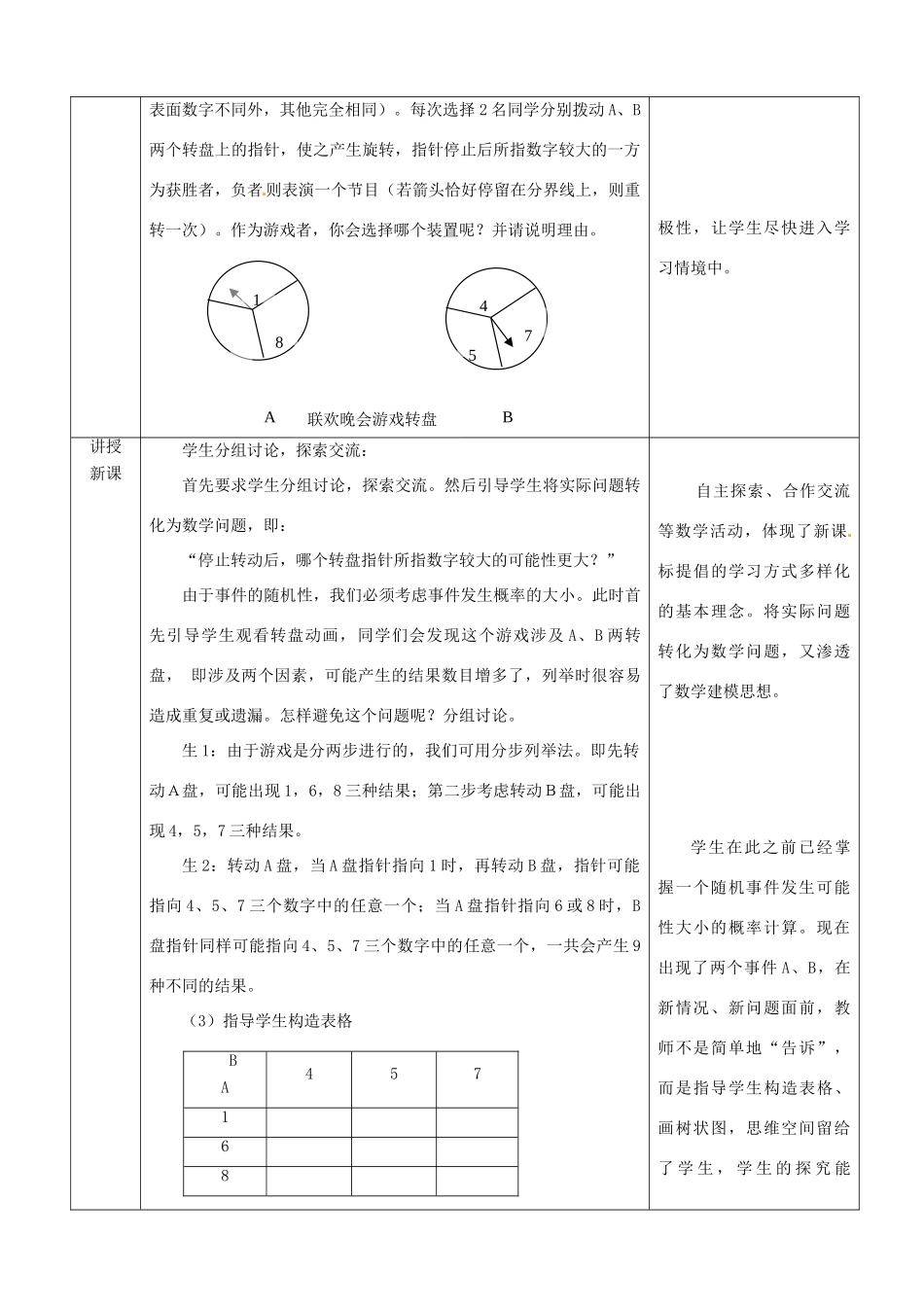
教学设计:等可能情形下的概率计算(第二课时)课题课题:28.2等可能情形下的概率计算(第二课时)教材:沪科版九年义务教育九年级数学(下)执教教师司擎天,马鞍山市外国语学校执教时间下午第一节课.时间:45分钟学情介绍1.学生通过近三年的学习,对事件发生的可能性大小已经有了较为清晰的认识,但对如何分析事件,计算概率尚有困难。2.由于本节课内容非常贴近生活,因此丰富的问题情境会激发学生浓厚的兴趣,但学生过去的生活经验会对这节课的学习带来障碍。教学目标1.在解决实际问题的过程中,体会随机的思想,进一步理解概率的意义。2.通过列表法、画树状图法探究计算概率的方法。3.经历实验、列表、统计、运算、设计等活动,学生在具体情境中分析事件,计算其发生的概率。渗透数形结合,分类讨论,由特殊到一般的思想,提高分析问题和解决问题的能力。4.通过丰富的数学活动,体验数学活动充满着探索和创造,体会数学的应用价值,培养积极思维的学习习惯。教学重点计算简单事件概率的方法;随机观念的培养.教学难点数学模型的建立,较复杂事件概率的计算。教学方法创设问题情境,引导学生把实际问题转化为数学问题并感悟其转化过程,通过师生共同对具体问题的分析,找出解决问题的方法.启发、诱导学生解决问题.教学环节课堂教学实录设计理念新课引入1.创设情景,发现新知引例:为活跃联欢晚会的气氛,组织者设计了以下转盘游戏:A、B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是1,6,8,转盘B上的数字分别是4,5,7(两个转盘除引例贴近学生生活实际,以联欢晚会为背景,创设转盘游戏引入,学生喜闻乐见,能激发学生的求知欲,调动学生学习积表面数字不同外,其他完全相同)。每次选择2名同学分别拨动A、B两个转盘上的指针,使之产生旋转,指针停止后所指数字较大的一方为获胜者,负者则表演一个节目(若箭头恰好停留在分界线上,则重转一次)。作为游戏者,你会选择哪个装置呢?并请说明理由。极性,让学生尽快进入学习情境中。讲授新课学生分组讨论,探索交流:首先要求学生分组讨论,探索交流。然后引导学生将实际问题转化为数学问题,即:“停止转动后,哪个转盘指针所指数字较大的可能性更大?”由于事件的随机性,我们必须考虑事件发生概率的大小。此时首先引导学生观看转盘动画,同学们会发现这个游戏涉及A、B两转盘,即涉及两个因素,可能产生的结果数目增多了,列举时很容易造成重复或遗漏。怎样避免这个问题呢?分组讨论。生1:由于游戏是分两步进行的,我们可用分步列举法。即先转动A盘,可能出现1,6,8三种结果;第二步考虑转动B盘,可能出现4,5,7三种结果。生2:转动A盘,当A盘指针指向1时,再转动B盘,指针可能指向4、5、7三个数字中的任意一个;当A盘指针指向6或8时,B盘指针同样可能指向4、5、7三个数字中的任意一个,一共会产生9种不同的结果。(3)指导学生构造表格自主探索、合作交流等数学活动,体现了新课标提倡的学习方式多样化的基本理念。将实际问题转化为数学问题,又渗透了数学建模思想。学生在此之前已经掌握一个随机事件发生可能性大小的概率计算。现在出现了两个事件A、B,在新情况、新问题面前,教师不是简单地“告诉”,而是指导学生构造表格、画树状图,思维空间留给了学生,学生的探究能168A457B联欢晚会游戏转盘BA457168(4)学生填写表格,通过观察与计算,得出结论(即列表法)从表中可以发现:A盘数字大于B盘数字的结果共有5种。∴P(A数较大)=,P(B数较大)=.∴P(A数较大)>P(B数较大)∴选择A装置的获胜可能性较大。在学生填写表格过程中,注意向学生强调数对的有序性。还有别的解决办法吗?(5)指导学生画树状图由图知:可能的结果为:(1,4),(1,5),(1,7),(6,4),(6,5),(6,7),(8,4),(8,5),(8,7)。共计9种。∴P(A数较大)=,P(B数较大)=.∴P(A数较大)>P(B数较大)∴选择A装置的获胜可能性较大。然后,引导学生对所画图形进行观察:若将图形倒置,你会联想到什么?这个图形很像一棵树,所以称为树状图(在幻灯片上放映)。列表和树状图是列举法求概率的两种常用的方法。...