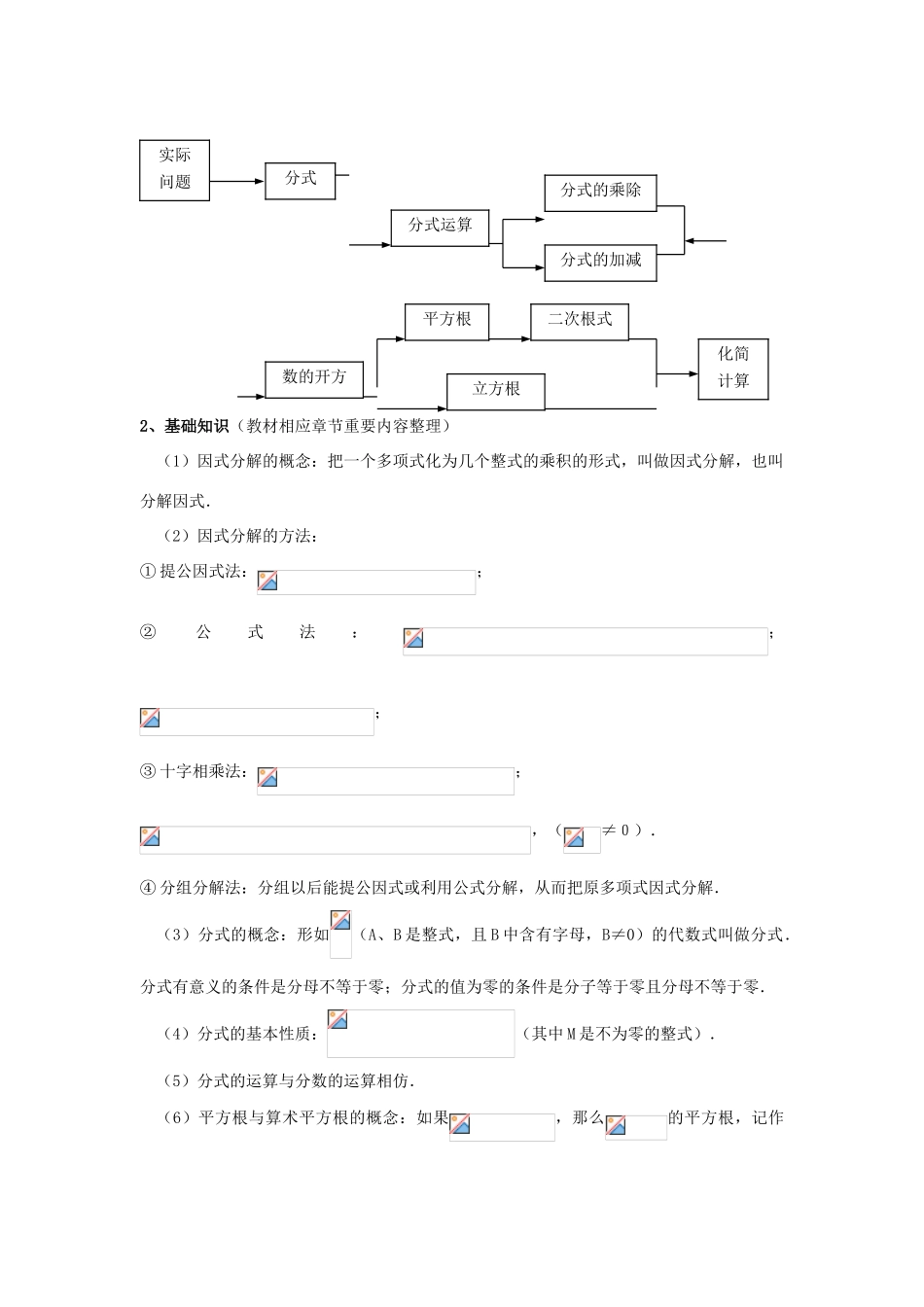
二、因式分解、分式、数的开方(3课时)教学目标:1.掌握本部分的知识结构图.基本概念的掌握要到位,不仅要理解更要会运用,复习时应要求学生先观察后动手,并保证较高的正确率。2.让学生自己总结交流所学内容,发展学生的语言表达能力和合作交流能力.3.通过学生自己归纳总结本部分内容,使他们在动手操作方面,探索研究方面,语言表达方面,分类讨论、归纳等方面都有所发展.教学重点与难点重点:复习性质、公式、法则时,要注意运用的条件,并重视对典型例题的变式训练,以达到熟悉运用公式、法则,提高运算能力的目的..难点:复习性质、公式、法则时,要注意运用的条件,并重视对典型例题的变式训练,以达到熟悉运用公式、法则,提高运算能力的目的.教学时间:3课时因式分解、分式、数的开方本单元在第一轮复习时大约需要3课时,其中包括单元测试.下表为复习内容及课时安排:课时数内容1因式分解1分式1数的开方因式分解、分式、数的开方单元测试与评析教学过程:【知识回顾】1、知识脉络(教材相应章节重要内容的结构与联系)因式分解提公因式法公式法分组分解法十字相乘法分式的基本性质通分约分2、基础知识(教材相应章节重要内容整理)(1)因式分解的概念:把一个多项式化为几个整式的乘积的形式,叫做因式分解,也叫分解因式.(2)因式分解的方法:①提公因式法:;②公式法:;;③十字相乘法:;,(≠0).④分组分解法:分组以后能提公因式或利用公式分解,从而把原多项式因式分解.(3)分式的概念:形如(A、B是整式,且B中含有字母,B≠0)的代数式叫做分式.分式有意义的条件是分母不等于零;分式的值为零的条件是分子等于零且分母不等于零.(4)分式的基本性质:(其中M是不为零的整式).(5)分式的运算与分数的运算相仿.(6)平方根与算术平方根的概念:如果,那么的平方根,记作实际问题分式分式运算分式的乘除分式的加减数的开方平方根二次根式立方根化简计算,其中叫做的算术平方根.(7)立方根的概念:如果那么叫做的立方根,记为(8)二次根式概念:形如的式子叫二次根式.(9)最简二次根式:满足下列两个条件,被开方数的因数是整数,因式是整式;被开方数中不含有能开得尽方的因数或因式,这样的二次根式叫做最简二次根式.(10)同类二次根式:把几个二次根式化为最简二次根式以后,如果被开方数相同,那么这几个二次根式叫做同类二次根式.(11)相关性质:;.(12)二次根式的运算:①加、减运算:先把每个二次根式化为最简二次根式,然后再合并同类二次根式.②乘、除运算:是积、商性质的逆向应用.运算结果中每一个二次根式都应是最简二次根式.3、能力要求例1在二次根式①,②,③,④是同类二次根式的是().A.①③B.②③C.①④D.③④【分析】解答本题的关鍵是能正确化简题中的四个二次根式,然后根据被开方数是否相同来选择与是否为同类二次根式.【解】 .∴与是同类二次根式的是①④,故答案选项C.【说明】最简二次根式、同类二次根式是本节内容两个重要概念,正确理解这两个概念,是进行二次根式加减运算的前提,因此在总复习时,应加强二次根式的化简的习题训练.例2把下列各式因式分解:(1)(2)(3)【分析】(1)本题在进行因式分解时,不能直接提公因式或用公式法来分解,因此考虑用分组分解法.在分组时,尝试第一、第二两项分在一组,第三、第四两项分在另一组后不能继续分解,因此把第一、第四两项结合,第二、第三两项结合,通过提公因式后来实现因式分解.(2)把化为,把化为,然后直接利用立方差公式来进行因式分解.(3)对于二次三项式的因式分解,常常考虑用十字相乘法来分解.【解】(1)原式=.(2)原式=(2x)3-=(2x-)(4x2++.(3)原式=.【说明】华师版义务教育新课标实验教材中的因式分解要求偏低.事实上,让学生掌握十字相乘法分解因式,对于灵活解一元二次方程、解一元二次不等式等非常有用;另外,分组是数学中的一种重要的解题思想方法,对于不能直接提公因式、利用公式来分解因式的多项式,可以尝试用分组分解法来进行因式分解.对于立方和(差)公式,在中考总复习时要补充...