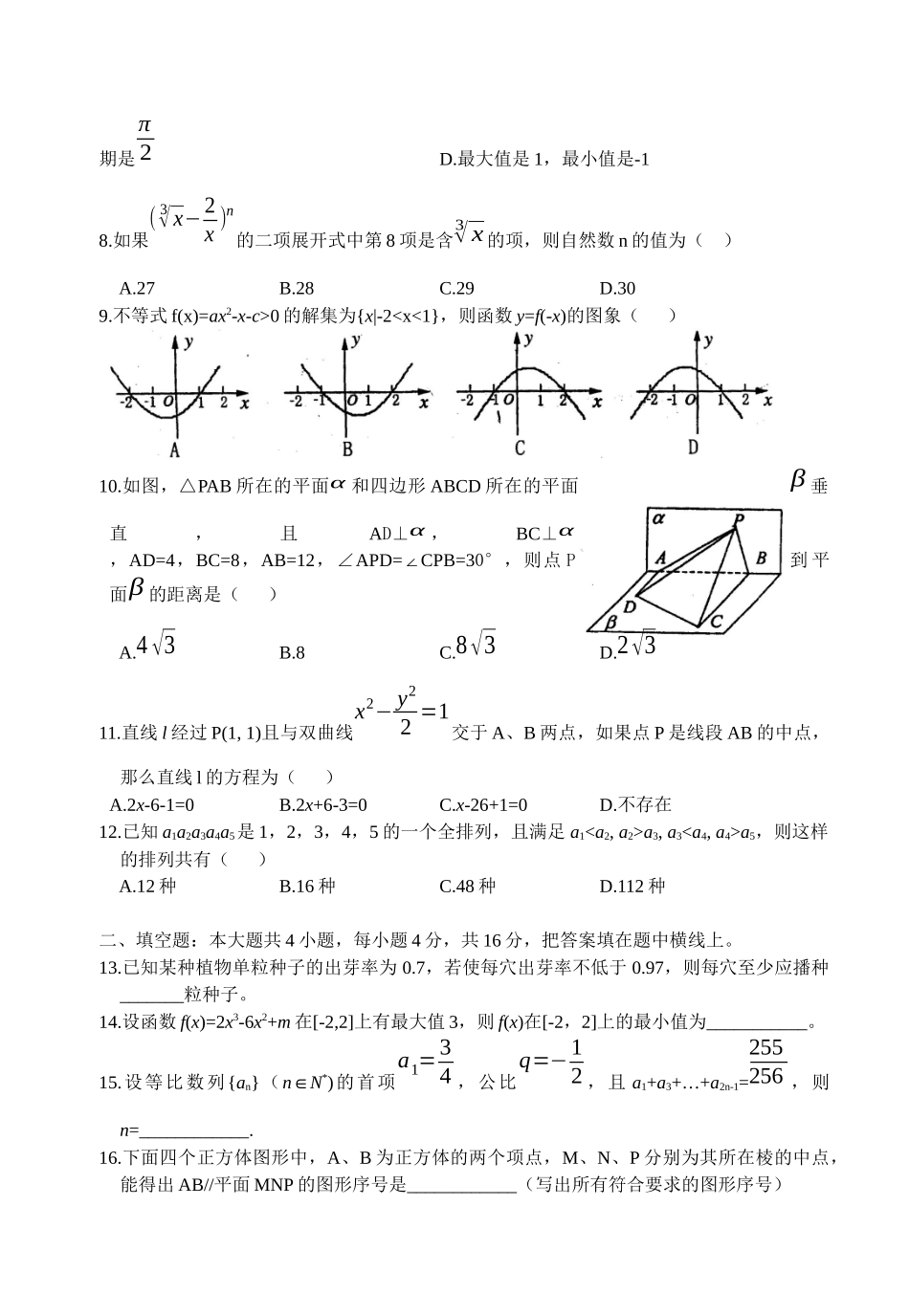
河南省郑州市2007年高中毕业班第三次质量预测文科数学(必修+选修Ⅰ)参考公式:如果事件A、B互斥,那么P(A+B)=P(A)+P(B)如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1−P)n−k球的表面积公式:S球=4πR2(其中R表示球的半径);球的体积公式:V=43πR3(其中R表示球的半径)。一、选择题1.已知A={x||x−12|≤32},B={x|4x-x2>0},则A∩B=()A.(0,2]B.[-1,0)C.[2,4)D.[1,4)2.若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角是()A.30°B.60°C.120°D.150°3.设f−1(x)是f(x)=log2x的反函数,若f−1(a)⋅f−1(b)=8,则f(a+b)的值为()A.log23B.1C.2D.34.“p或q是真命题”是“p且q是假命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.一个项数为偶数的等差数列,奇数项和、偶数项和分别为24和30,若最后一项超过第一项10.5,那么,该数列的项数为()A.18B.12C.10D.86.过曲线y=x2-2x-1上一点(2,-1),且与曲线相切的直线方程为()A.2x-y-5=0B.2x+y-3=0C.x+2y=0D.x-2y-4=07.关于函数y=2sin(2x+π6)的叙述正确的是()A.在区间[−π3+kπ,π6+kx](k∈Z)上是增函数B.是奇函数C.周期是π2D.最大值是1,最小值是-18.如果(3√x−2x)n的二项展开式中第8项是含3√x的项,则自然数n的值为()A.27B.28C.29D.309.不等式f(x)=ax2-x-c>0的解集为{x|-2
a3,a3a5,则这样的排列共有()A.12种B.16种C.48种D.112种二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。13.已知某种植物单粒种子的出芽率为0.7,若使每穴出芽率不低于0.97,则每穴至少应播种_______粒种子。14.设函数f(x)=2x3-6x2+m在[-2,2]上有最大值3,则f(x)在[-2,2]上的最小值为___________。15.设等比数列{an}(n∈N*)的首项a1=34,公比q=−12,且a1+a3+…+a2n-1=255256,则n=____________.16.下面四个正方体图形中,A、B为正方体的两个项点,M、N、P分别为其所在棱的中点,能得出AB//平面MNP的图形序号是____________(写出所有符合要求的图形序号)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。17.(本小题满分12分)已知函数f(x)=cos2x−2sinxcosx−sin2(x∈R).(I)画出函数y=f(x)在区间[0,π]上的简图;(II)说明函数y=f(x)的图象可由y=√2cosx的图象经过怎样的变换而得到。18.(本小题满分12分)某运动员小马,欲取得08年奥运会参赛资格,需要参加三个阶段比赛,第一、第二阶段各有两个对手,必须都获胜,方可进入下一个阶段的比赛,第三阶段有三个对手,只要取胜两人就可以取得奥运会的参赛资格(先赢两场者第三场不用比赛),每阶段获胜分别可得1万元、3万元、9万元的资金(不重复获奖),小马对三个阶段每位运动员获胜的概率依次为45,34,23,假定与每个选手比赛胜负相互独立。(I)求小马通过第一阶段但未通过第二阶段的概率;(II)求小马获得资金为3万元的概率。19.(本小题满分12分)如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为√32的菱形。∠ACC1为锐角,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AC=1.(I)求异面直线BB1与AC所成的角;(II)求侧面BCC1B1与侧面ACC1A1所成二面角的大小。20.(本小题满分12分)已知数列{an}的各项均为正数,a1=1,对任意nN∈*,an+1=2an+1,bn=log2(an+1)都成立。(I)求数列{an},{bn}的通项公式;(II)证明:对于任意nN∈*,都有1b12+1b22+1b32+⋯+1bn2<2成立。21.(本小题满分12分)设抛物线y=12x2的焦点为F,准线为l,过点F的直线斜率为k且与抛物线交于A,B两点,P在准线...