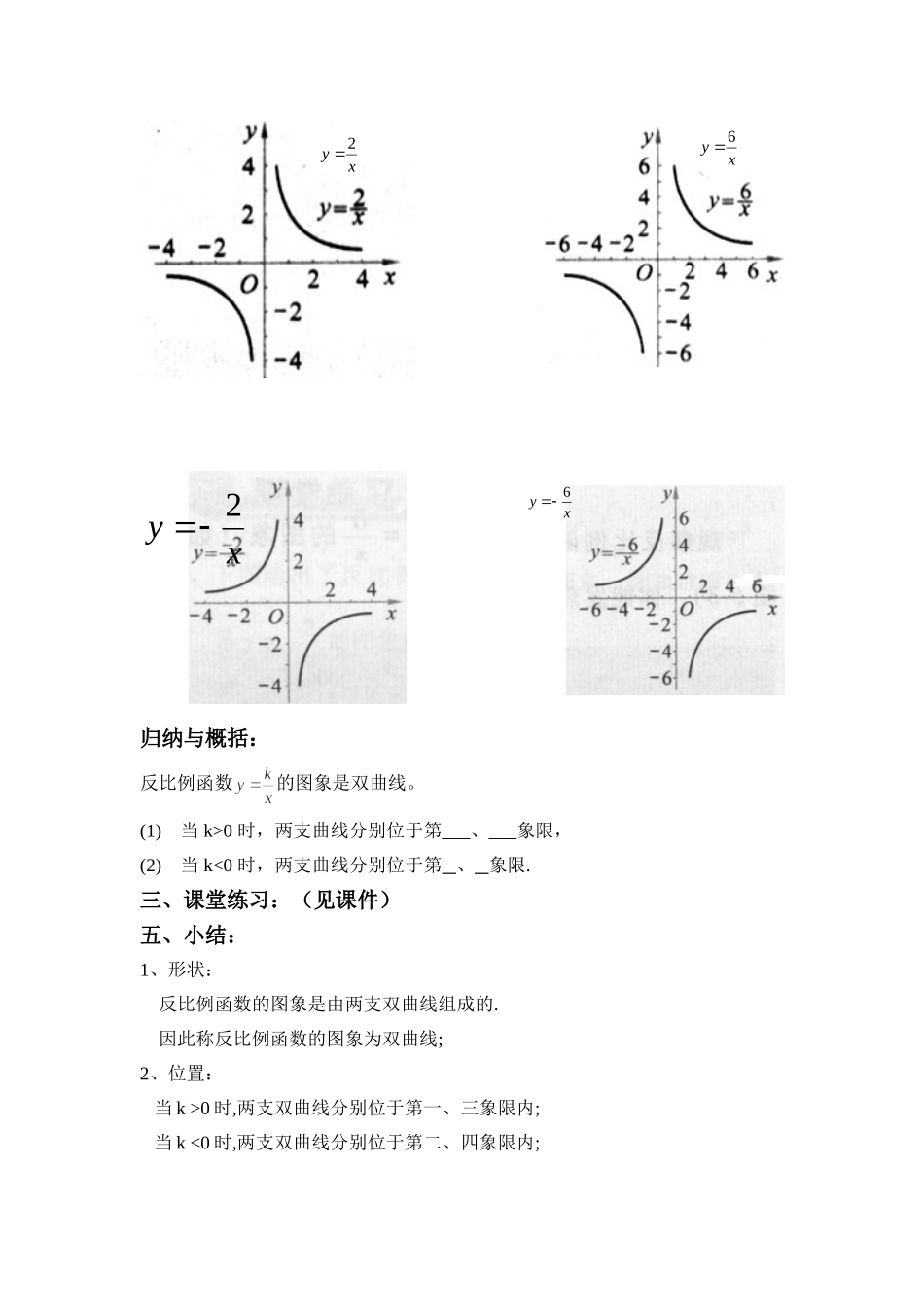
反比例函数的图象与性质(1)教学目标:1.进一步熟悉作函数图象的主要步骤,会作反比例函数的图象.2.逐步提高从函数图象小获取信息的能力,探索并掌握反比例函数的主要性质.3.通过学生自己动手列表、描点、连线,提高学生的作图能力;通过观察图象,概括反比例函数的有关性质,训练学生的概括、总结能力.教学重点:画反比例函数的图象;并从函数图象中获取信息,探索并研究反比例函数的主要性质.教学难点:反比例函数的图象特点及性质的探究.教学手段:多媒体课件教学内容及过程:一、课前热身:1、反比例函数的一般形式是:。2、反比例函数中,自变量x的取值范围是:。3、已知,若k>0,则x与y符号k<0,则x与y符号4、一次函数y=kx+b(k≠0)的图象是。5、画函数图象的三大步骤是:①,②,③。二、新知探究1、作反比例函数的图象。思考:(1)这个函数中自变量x的取值范围是什么?(2)自变量x的取值怎样取较好?(3)由学生列表、描点、连线。(4)出示3则错误的画图,让学生分析错误的原因。(5)给出正确的作图,再由学生改正自己的画图。(6)画反比例函数的图像应注意什么?列表时:连线时:2、画出函数的图象.讨论与交流:相同点:1.图像分别都是由两支曲线组成.它们都不与坐标轴相交.2.两个函数图像自身都是轴对称图形,它们各有两条对称轴.3.两个函数图像自身都是中心对称图形,对称中心是坐标原点.不同点:的两支曲线分别位于第一、三象限内;两支曲线分别位于第二、四象限内。2、请再观察下列函数的图象,并进行总结.归纳与概括:反比例函数的图象是双曲线。(1)当k>0时,两支曲线分别位于第___、___象限,(2)当k<0时,两支曲线分别位于第、象限.三、课堂练习:(见课件)五、小结:1、形状:反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;2、位置:当k>0时,两支双曲线分别位于第一、三象限内;当k<0时,两支双曲线分别位于第二、四象限内;xy2xy6xy2xy6教学后记:学生能准确地根据k的符号判断双曲线所在的象限,但画反比例函数的图像不熟练,不规范,对稍有综合的题目还不会做,知识遗忘太严重。