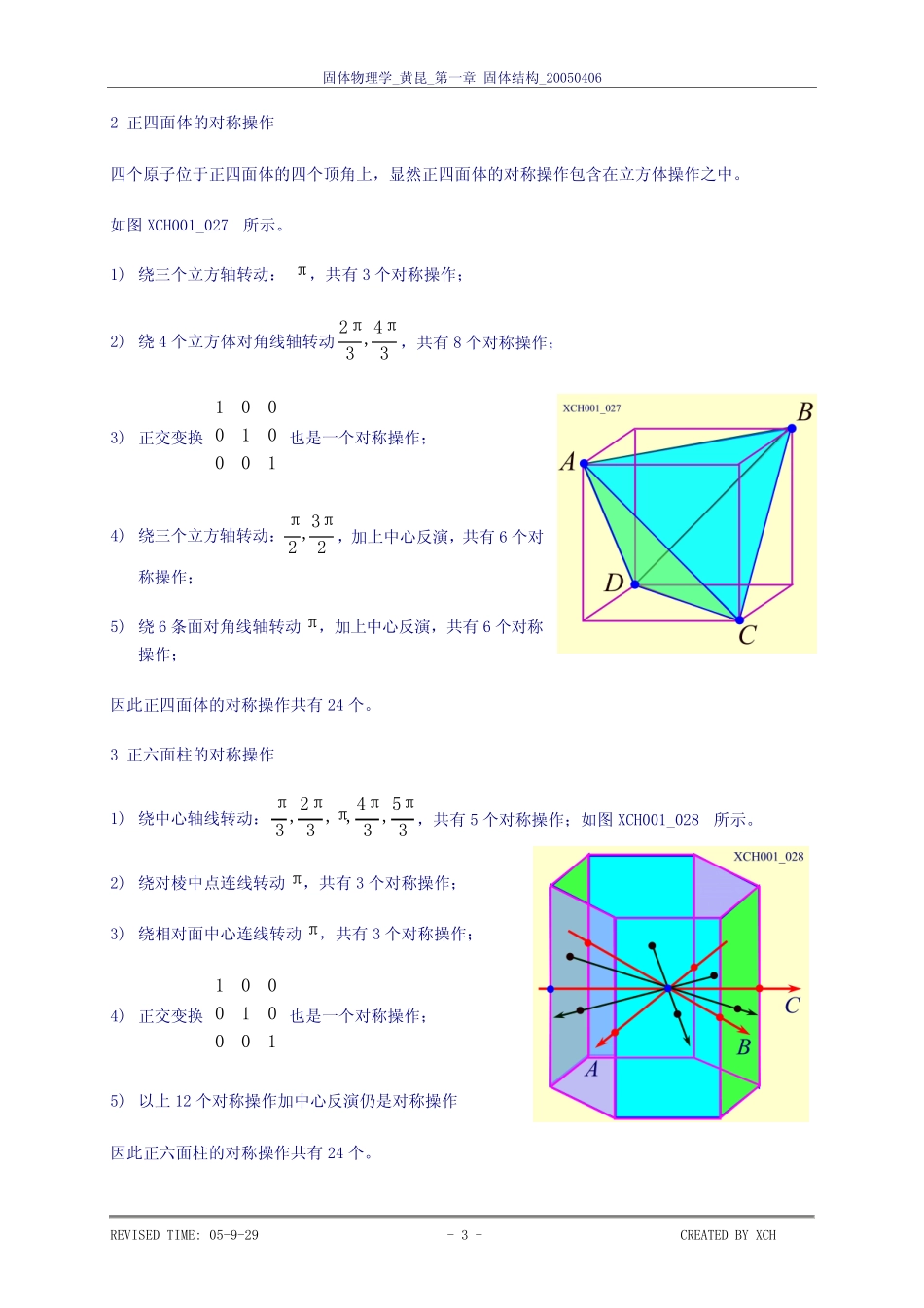
固体物理学_黄昆_第一章固体结构_200504062正四面体的对称操作四个原子位于正四面体的四个顶角上,显然正四面体的对称操作包含在立方体操作之中。如图XCH001_027所示。1)绕三个立方轴转动:π,共有3个对称操作;2)绕4个立方体对角线轴转动34,32ππ,共有8个对称操作;3)正交变换也是一个对称操作;⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛1000100014)绕三个立方轴转动:23,2ππ,加上中心反演,共有6个对称操作;5)绕6条面对角线轴转动π,加上中心反演,共有6个对称操作;因此正四面体的对称操作共有24个。3正六面柱的对称操作1)绕中心轴线转动:35,34,,32,3πππππ,共有5个对称操作;如图XCH001_028所示。2)绕对棱中点连线转动π,共有3个对称操作;3)绕相对面中心连线转动π,共有3个对称操作;4)正交变换也是一个对称操作;⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛1000100015)以上12个对称操作加中心反演仍是对称操作因此正六面柱的对称操作共有24个。REVISEDTIME:05-9-29-3-CREATEDBYXCH固体物理学_黄昆_第一章固体结构_200504064对称素为简洁明了地概括一个物体的对称性,不去一一列举所有的对称操作,而是描述它所具有的“对称素”。对称素就是一个物体的旋转轴,以及旋转-反演轴。一个物体绕某一个转轴转动nπ2,以及其倍数不变时,称该轴为物体n重旋转轴,计为n。一个物体绕某一个转轴转动nπ2加上中心反演的联合操作,以及其联合操作的倍数不变时,称该轴为物体n重旋转-反演轴轴,计为n。+立方体——立方轴(23,,2πππ)为4重轴,计为4;同时也是4重旋转-反演轴,计为4;——面对角线(π)为2重轴,计为2;同时也是2重旋转-反演轴,计为2;——体对角线轴(34,32ππ)为3重轴,计为3;同时也是3重旋转-反演轴,计为3;+正四面体——立方轴是4重旋转-反演轴,但不是4重轴;——面对角线是2重旋转-反演轴,但不是2重轴;——体对角线轴是3重轴,但不是3重旋转-反演轴。+对称素2,它的含义:先绕轴转动π,再作中心反演,如图XCH001_029所示。A’’点实际上是A点在通过中心垂直于转轴的平面M的镜像,表明对称素2存在一个对称面M。所以称对称素2为镜面,用σorm,表示。+对称操作群——一个物体的全部对称操作构成一个对称操作群5群的基本知识REVISEDTIME:05-9-29-4-CREATEDBYXCH固体物理学_黄昆_第一章固体结构_20050406群代表一组“元素”的集合,G≡{E,A,B,C,D……}这些“元素”被赋予一定的“乘法法则”,满足下列性质:1)集合G中任意两个元素的“乘积”仍为集合内的元素,即,若A,B∈G,则AB=C∈G.叫做群的封闭性。2)存在单位元素E,使得所有元素满足:AE=A3)对于任意元素A,存在逆元素A-1,有:AA-1=E4)元素间的“乘法运算”满足结合律:A(BC)=(AB)C+几个简单的群1)所有正实数(0除外)的集合,以普通乘法为运算法则,组成正实数群。2)所有整数的集合,以加法为运算法则,组成整数群。一个物体全部对称操作的集合满足上述群的定义,其运算法则就是连续操作。单位元素:不动操作任意元素的逆元素:绕转轴θ角度,其逆操作为绕转轴θ−角度;中心反演的逆操作仍是中心反演;连续进行A和B操作,相对于C操作,如图XCH_001_030所示。A操作:绕OA轴转动2π,S点转到T’点;B操作:绕OC轴转动2π,T’点转到S点;上述操作中S和O没动,而T点转动到T’点。相当于一个操作C:绕OS轴转动32π表示为:—群的封闭性BAC=可以证明:-满足结合律CABBCA)()(=REVISEDTIME:05-9-29-5-CREATEDBYXCH固体物理学_黄昆_第一章固体结构_200504066立方对称晶体的介电系数∑=ββαβαεED,βααβεε=——βα,表示沿X,Y,Z轴的分量,选取X,Y,Z轴为立方体的三个立方轴方向。如图XCH001_037所示。假设电场EK沿Y轴方向:0,===zxyEEEE∑=ββαβαεED,xxxxyxzyyxyyyzzzxzyzzDEDEDEεεεεεεεεε⎛⎞⎛⎞⎛⎜⎟⎜⎟⎜=⎜⎟⎜⎟⎜⎜⎟⎜⎜⎟⎝⎠⎝⎝⎠xyz⎞⎟⎟⎟⎠可以写成:EDxyxε=,EDyyyε=,EDzyzε=现将晶体和电场同时绕Y轴转动2π,DK也作相应的转动。如图XCH001_037所示。yyzxxz→−→→,,:EDDzyzxε==',EDDyyyyε==',EDDxyxzε−=−='该转动的实施,电场没有变,同时又是一个对称操作,晶体转动前...