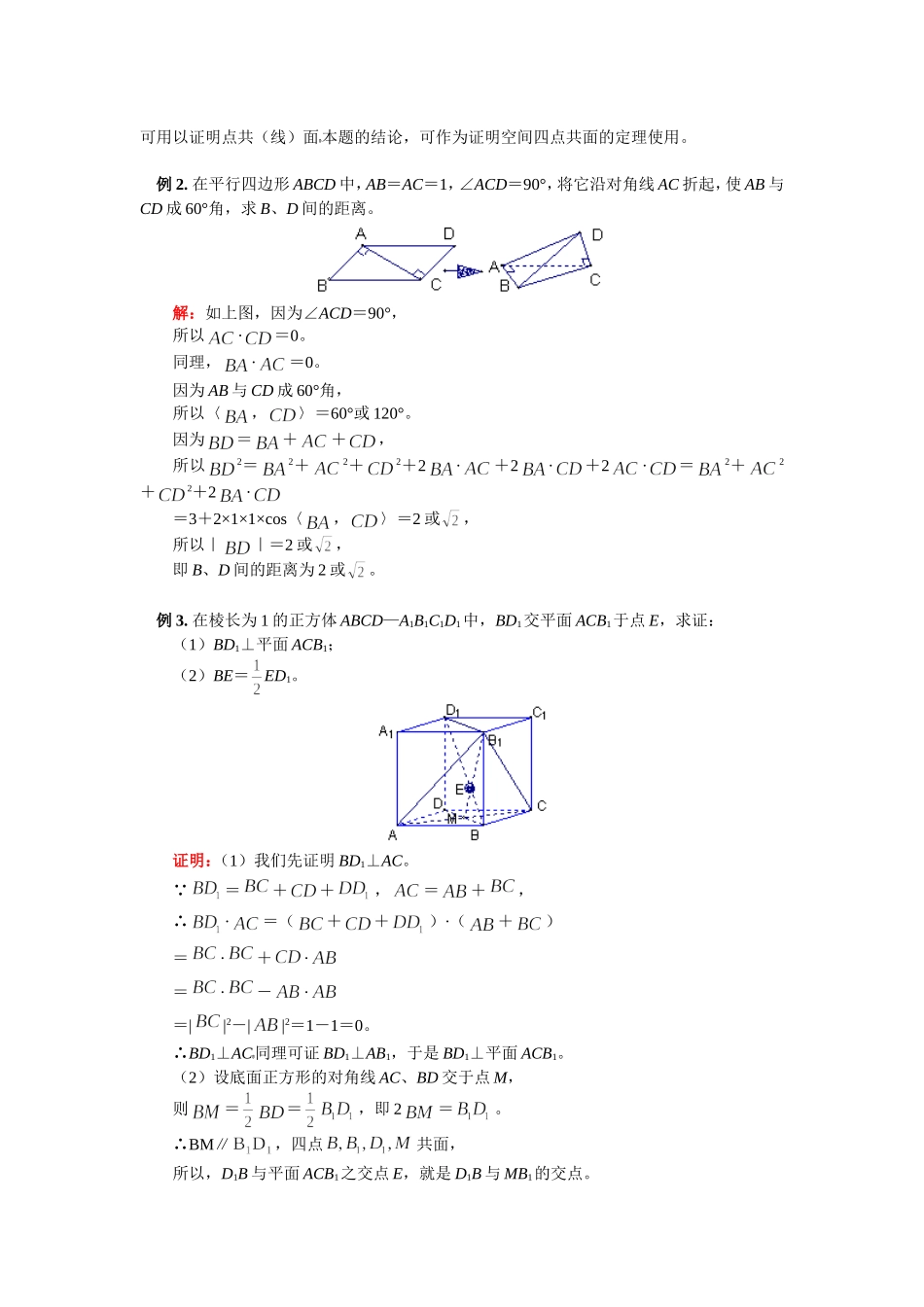
高三数学空间向量苏教版【本讲教育信息】一.教学内容:空间向量二.教学目标:1、理解空间向量的概念,掌握空间向量的加法、减法和数乘。2、了解空间向量的基本定理;3、掌握空间向量的数量积的定义及其性质;4、理解直线的方向向量、平面的法向量、向量在平面内的射影等概念。5、掌握空间向量平行、垂直的条件及三个向量共面及四点共面的条件。三.知识要点:1.空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。注:⑴空间的一个平移就是一个向量。⑵向量一般用有向线段表示。同向等长的有向线段表示同一或相等的向量。⑶空间的两个向量可用同一平面内的两条有向线段来表示。2.空间向量的运算空间向量的加法、减法与数乘向量运算:;;运算律:⑴加法交换律:⑵加法结合律:⑶数乘分配律:3.平面向量共线定理方向相同或者相反的非零向量叫做平行向量。由于任何一组平行向量都可以平移到同一条直线上,所以平行向量也叫做共线向量。向量与非零向量共线的充要条件是有且只有一个实数λ,使=λ。4.共线向量如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量。平行于记作。当我们说向量、共线(或//)时,表示、的有向线段所在的直线可能是同一直线,也可能是平行直线。5.共线向量定理:空间任意两个向量、(≠),//的充要条件是存在实数λ,使=λ。推论:如果为经过已知点A且平行于已知非零向量的直线,那么对于任意一点O,点P在直线上的充要条件是存在实数t满足等式。。其中向量叫做直线的方向向量。6.空间直线的向量参数表示式:或,中点公式:7.向量与平面平行:已知平面和向量,作,如果直线平行于或在内,那么我们说向量平行于平面,记作:。通常我们把平行于同一平面的向量,叫做共面向量。说明:空间任意的两向量都是共面的。8.共面向量定理:如果两个向量不共线,与向量共面的充要条件是存在实数使。推论:空间一点位于平面内的充分必要条件是存在有序实数对(),使①或对空间任一点,有②或③上面①式叫做平面的向量表达式。9.空间向量基本定理:如果三个向量不共面,那么对空间任一向量,存在一个唯一的有序实数组(),使。若三向量不共面,我们把叫做空间的一个基底,叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。推论:设是不共面的四点,则对空间任一点,都存在唯一的三个有序实数,使。10.空间向量的夹角及其表示:已知两非零向量,在空间任取一点,作,则叫做向量与的夹角,记作;且规定,显然有;若,则称与互相垂直,记作:。11.向量的模:设,则有向线段的长度叫做向量的长度或模,记作:。12.向量的数量积:已知向量,则叫做的数量积,记作,即。13.空间向量数量积的性质:(1)。(2)。(3)。14.空间向量数量积运算律:(1)(结合律)。(2)(交换律)。(3)(分配律)。【典型例题】例1.证明空间任意无三点共线的四点A、B、C、D共面的充分必要条件是:对于空间任一点O,存在实数x、y、z且x+y+z=1,使得=x+y+z。分析:要寻求四点A、B、C、D共面的充要条件,自然想到共面向量定理。解:依题意知,B、C、D三点不共线,则由共面向量定理的推论知:四点A、B、C、D共面对空间任一点O,存在实数x1、y1,使得=+x1+y1=+x1(-)+y1(-)=(1-x1-y1)+x1+y1,取x=1-x1-y1、y=x1、z=y1,则有=x+y+z,且x+y+z=1。点评:向量基本定理揭示了向量间的线性关系,即任一向量都可由基向量唯一的线性表示,为向量的坐标表示奠定了基础。共(线)面向量基本定理给出了向量共(线)面的充要条件,可用以证明点共(线)面新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆本题的结论,可作为证明空间四点共面的定理使用。例2.在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B、D间的距离。解:如上图,因为∠ACD=90°,所以·=0。同理,·=0。因为AB与CD成60°角,所以〈,〉=60°或120°。因为=++,所以2=2+2+2+2·+2·...