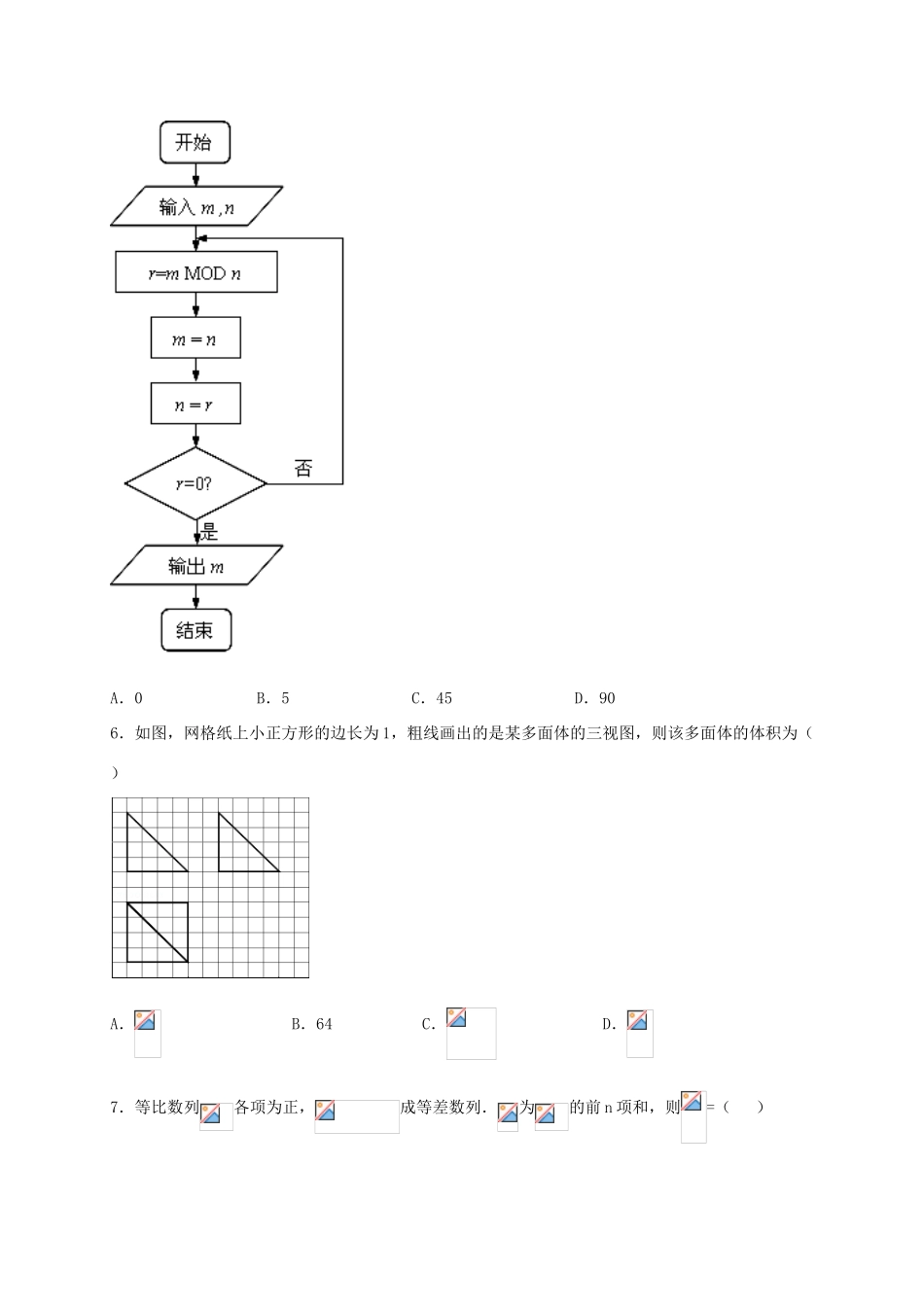
新疆兵团农二师华山中学2017届高三数学上学期学前考试试题文一、选择题(单选题,每题5分)1.已知集合,则集合为()A.B.C.D.2.给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.若复数的实部与虚部互为相反数,则()A.B.C.D.24.下列函数既是奇函数,又在区间上单调递减的是()(A)(B)(C)(D)5.这个程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示除以的余数),若输入的,分别为495,135,则输出的=()A.0B.5C.45D.906.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为()A.B.64C.D.7.等比数列各项为正,成等差数列.为的前n项和,则=()A.2B.C.D.8.已知,满足约束条件,则的最大值为()A.B.C.D.9.若平面向量满足,则与的夹角是()A.B.C.D.10.函数()的单调递减区间为()A.B.C.D.11.已知离心率为的双曲线和离心率为的椭圆有相同的焦点是两曲线的一个公共点,若,则等于()A.B.C.D.312.若曲线在上存在垂直轴的切线,则实数取值范围为()A.B.C.D.二、填空题(每题5分)13.cos2–sin2=.14.所有棱长均为的正四棱锥的外接球的表面积等于.15.给出下列四个命题:(1)若,则;(2)若,则;(3),则;(4)若,则.其中正确命题的是.(填所有正确命题的序号)16.已知函数,若正实数满足,则的最小值是.三、解答题(要有必要的解答过程共70分)17.(本题满分12分)设a,b,c分别是△ABC的三个内角A、B、C所对的边,S是△ABC的面积,已知a=4,b=5,S=5.(1)求角C;(2)求c边的长度.18.(本题满分12分)某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:分数区间甲班频率乙班频率0.10.20.20.20.30.30.20.20.20.1(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;(Ⅱ)根据以上数据完成下面的×列联表:优秀不优秀总计甲班乙班总计在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?参考公式:,其中≥19.(本题满分12分)如图,直三棱柱ABCA1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥FAEC的体积.20.(本题满分12分)已知椭圆经过点,离心率为.(1)求椭圆的方程;(2)设直线与椭圆交于、,点关于轴的对称点(与不重合),则直线与轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.21.(本题满分12分)已知函数,曲线在点处的切线与直线垂直(其中为自然对数的底数).(1)求的解析式及单调递减区间;(2)是否存在常数,使得对于定义域内的任意,恒成立?若存在,求出的值;若不存在,请说明理由.22.(从下列两题中任选一道,本题满分12分)(1)在极坐标系中,直线的极坐标方程为,以极点为原点极轴为轴的正半轴建立平面直角坐标系,曲线的参数方程为为参数,且).(Ⅰ)写出直线的直角坐标方程和曲线的普通方程;(Ⅱ)若直线与曲线有两个公共点,求的取值范围.(2)已知函数.(Ⅰ)当时,解不等式;(Ⅱ)若存在满足,求的取值范围.参考答案1.D2.A3.C4.C5.C6.D7.C8.A9.D10.B11.A12.B13.14.15.(1)(2)(4)16.17.(1)由题知由S=absinC得,,解得,又C是△ABC的内角,所以或;(2)当时,由余弦定理得==21,解得;当时,=16+25+2×4×5×=61,解得.综上得,c边的长度是或.18.(Ⅰ)乙班参加测试的90分以上的同学有6人,记为A、B、C、D、E、F.成绩优秀的记为A、B.从这六名学生随机抽取两名的基本事件有:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个设事件G表示恰有一位学生成绩优秀,符合要求的事件有{A,C},{A,D},{A,E},{A,F}...