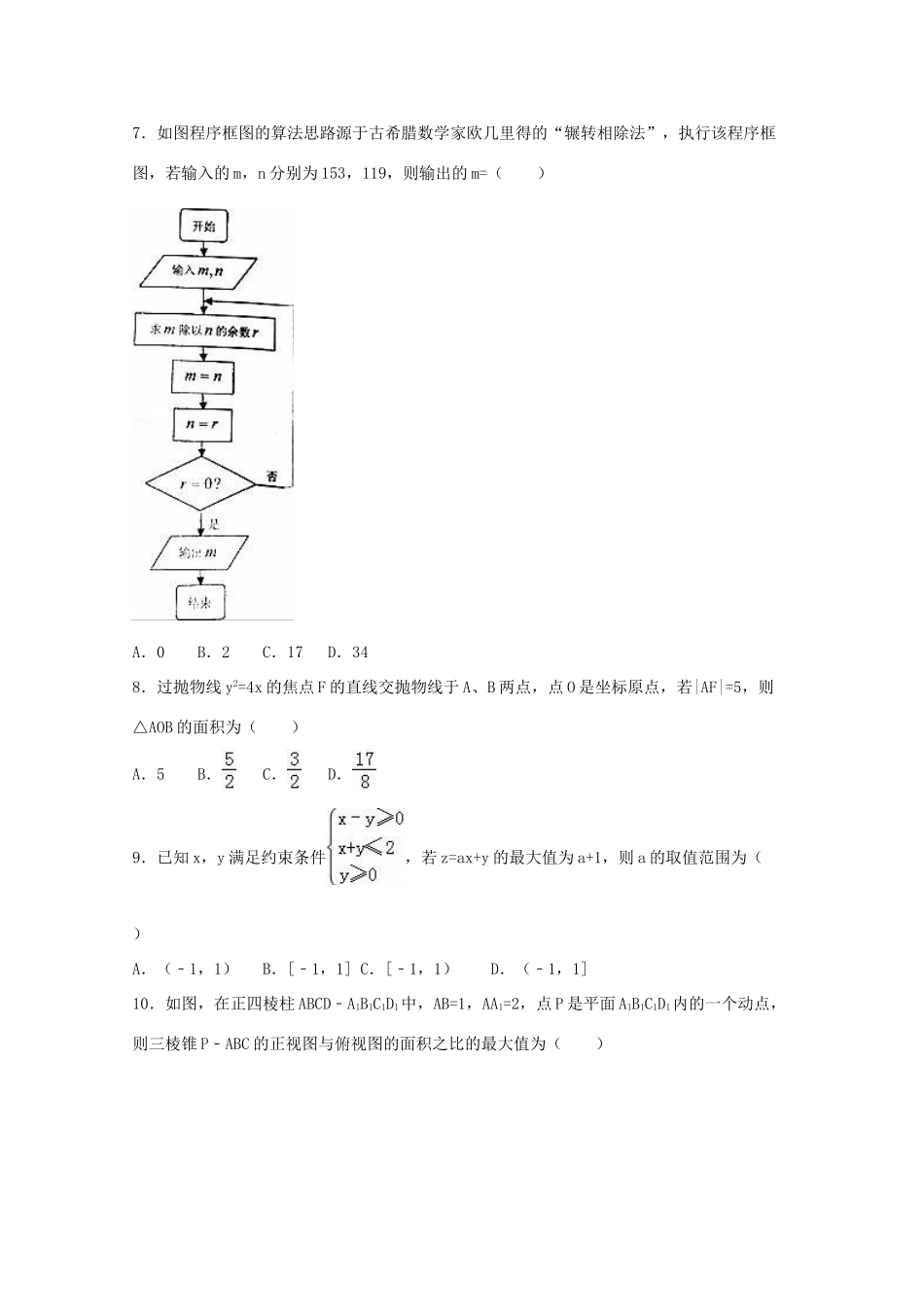
安徽师大附中2016年高考数学考前最后一卷(文科)(解析版)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x|x2+x﹣12≤0},N={y|y=3x,x≤1},则集合{x|x∈M且x∉N}为()A.(0,3]B.[﹣4,3]C.[﹣4,0)D.[﹣4,0]2.i为虚数单位,若,则|z|=()A.1B.C.D.23.已知命题p:函数f(x)=|cosx|的最小正周期为2π;命题q:函数y=x3+sinx的图象关于原点中心对称,则下列命题是真命题的是()A.p∧qB.p∨qC.(¬p)∧(¬q)D.p∨(¬q)4.若||=,||=2,(﹣)⊥,则,的夹角是()A.B.C.D.5.函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<)的图象如图所示,为了得到y=cos2x的图象,则只要将f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度6.已知等比数列{an}的前n项和为Sn,a1+a3=,且a2+a4=,则=()A.4n﹣1B.4n﹣1C.2n﹣1D.2n﹣17.如图程序框图的算法思路源于古希腊数学家欧几里得的“辗转相除法”,执行该程序框图,若输入的m,n分别为153,119,则输出的m=()A.0B.2C.17D.348.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为()A.5B.C.D.9.已知x,y满足约束条件,若z=ax+y的最大值为a+1,则a的取值范围为()A.(﹣1,1)B.[﹣1,1]C.[﹣1,1)D.(﹣1,1]10.如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=2,点P是平面A1B1C1D1内的一个动点,则三棱锥P﹣ABC的正视图与俯视图的面积之比的最大值为()A.1B.2C.D.11.在正方体ABCD﹣A1B1C1D1中,AB=2,点A,B,C,D在球O上,球O与BA1的另一个交点为E,且AE⊥BA1,则球O的表面积为()A.6πB.8πC.12πD.16π12.已知函数f(x)=x2﹣x﹣(x<0),g(x)=x2+bx﹣2(x>0),b∈R,若f(x)图象上存在A,B两个不同的点与g(x)图象上A′,B′两点关于y轴对称,则b的取值范围为()A.(﹣4﹣5,+∞)B.(4﹣5,+∞)C.(﹣4﹣5,1)D.(4﹣5,1)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设Sn为数列{an}的前n项和,若Sn=8an﹣1,则=.14.在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为.15.已知F1、F2是双曲线=1的焦点,PQ是过焦点F1的弦,且PQ的倾斜角为60°,那么|PF2|+|QF2|﹣|PQ|的值为.16.已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2﹣x﹣1|,则函数y=f(x)﹣1在区间[﹣2,4]上的零点个数为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在等比数列{an}中,a3=,S3=.(Ⅰ)求{an}的通项公式;(Ⅱ)记bn=log2,且{bn}为递增数列,若Cn=,求证:C1+C2+C3+…Cn<.18.国内某知名大学有男生14000人,女生10000人.该校体育学院想了解本校学生的运动状况,根据性别采取分层抽样的方法从全校学生中抽取120人,统计他们平均每天运动的时间,如表:(平均每天运动的时间单位:小时,该校学生平均每天运动的时间范围是[0,3])男生平均每天运动的时间分布情况:平均每天运动的时间[0,0.5)[0.5,1)[1,1.5)[1.5,2)[2,2.5)[2.5,3]人数212231810x女生平均每天运动的时间分布情况:平均每天运动的时间[0,0.5)[0.5,1)[1,1.5)[1.5,2)[2,2.5)[2.5,3]人数51218103y(Ⅰ)请根据样本估算该校男生平均每天运动的时间(结果精确到0.1);(Ⅱ)若规定平均每天运动的时间不少于2小时的学生为“运动达人”,低于2小时的学生为“非运动达人”.①请根据样本估算该校“运动达人”的数量;②请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘运动达人’与性别有关?”运动达人非运动达人总计男生女生总计参考公式:,其中n=a+b+c+d.参考数据:P(K2≥k0)0.100.050.0250.0100.0050.001k02.7063.8415.0246.6357.87910.82819.如图,四棱柱...