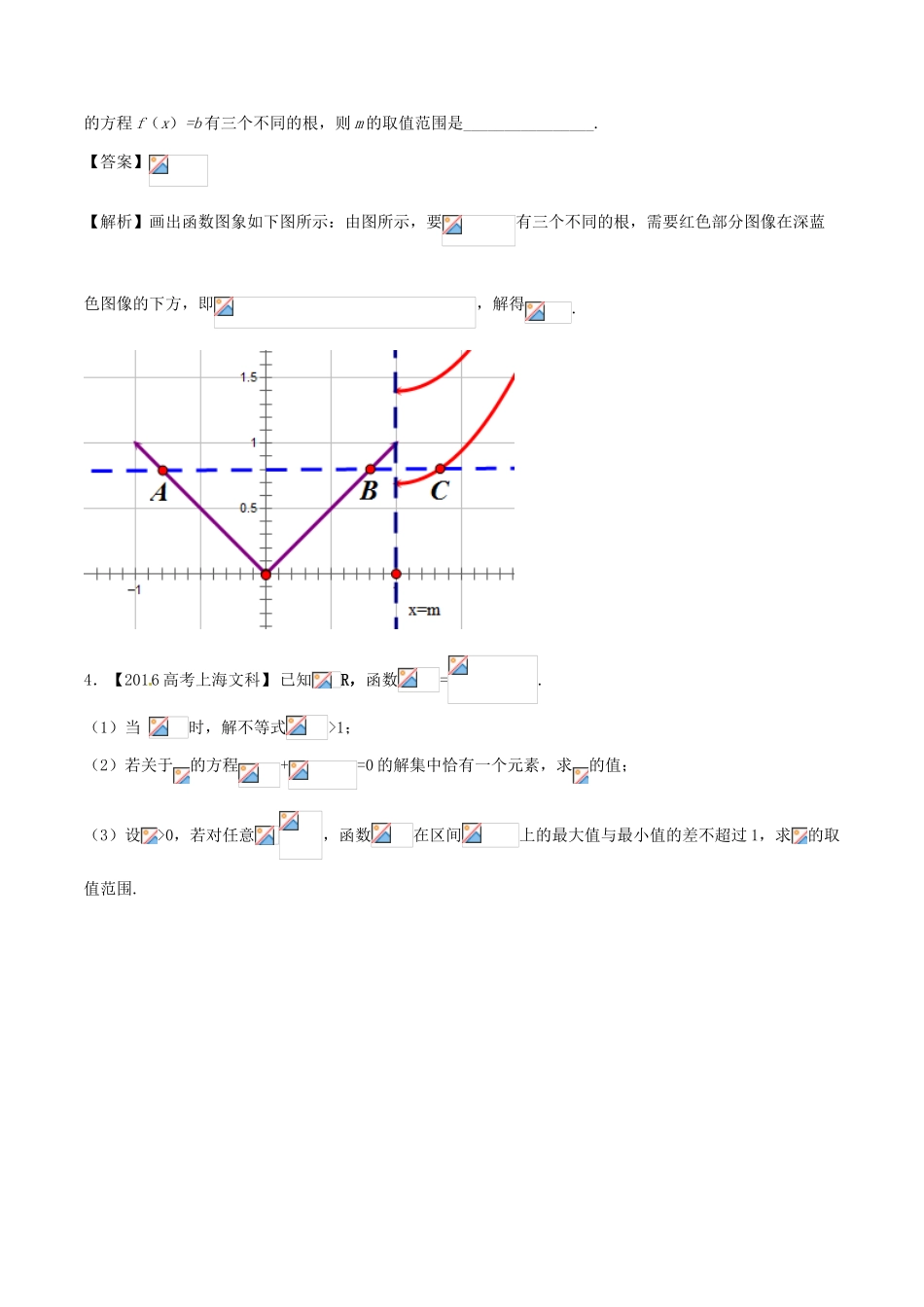
专题2.4函数图象与方程试题文【三年高考】1.【2016高考新课标1卷】函数在的图像大致为(A)(B)(C)(D)【答案】D2.【2016高考浙江文数】函数y=sinx2的图象是()【答案】D3.【2016高考山东文数】已知函数其中,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是________________.【答案】【解析】画出函数图象如下图所示:由图所示,要有三个不同的根,需要红色部分图像在深蓝色图像的下方,即,解得.4.【2016高考上海文科】已知R,函数=.(1)当时,解不等式>1;(2)若关于的方程+=0的解集中恰有一个元素,求的值;(3)设>0,若对任意,函数在区间上的最大值与最小值的差不超过1,求的取值范围.5.【2015高考上海,文8】方程的解为.【答案】2【解析】依题意,所以,,所以,解得或,当时,,所以,而,所以不合题意,舍去;当时,,所以,,,所以满足条件,所以是原方程的解.6.【2015高考浙江,文5】函数(且)的图象可能为()A.B.C.D.【答案】D【解析】因为,故函数是奇函数,所以排除A,B;取,则,故选D.7.【2015高考安徽,文10】函数的图像如图所示,则下列结论成立的是()(A)a>0,b<0,c>0,d>0(B)a>0,b<0,c<0,d>0(C)a<0,b<0,c<0,d>0(D)a>0,b>0,c>0,d<0【答案】A8.【2015高考天津,文8】已知函数,函数,则函数的零点的个数为()(A)2(B)3(C)4(D)5【答案】A9.【2015高考安徽,文14】在平面直角坐标系中,若直线与函数的图像只有一个交点,则的值为.【答案】【解析】在同一直角坐标系内,作出的大致图像,如下图:由题意,可知10.【2014高考北京卷文第6题】已知函数,在下列区间中,包含零点的区间是()A.B.C.D.【答案】C【解析】因为,,所以由根的存在性定理可知:选C.11.【2014高考天津卷卷文第14题】已知函数若函数恰有4个零点,则实数的取值范围为_______【答案】12.【2014高考重庆卷文第10题】已知函数内有且仅有两个不同的零点,则实数的取值范围是()A.B.C.D.【答案】A【解析】令,则问题转化为与的图象在内有且仅有两个交点;是一个分段函数,的图象是过定点的直线发上图所示,易求当直线与曲线在第三象限相切时,由图可知,或,故选A.21123442246【三年高考命题回顾】纵观前三年各地高考试题,对函数图象与方程这部分的考查,主要以图象的辨识与对称性以及利用图象研究函数的性质,方程,不等式的解是高考的热点,多以选择题、填空题的形式出现,属中低档题,主要考查基本初等函数的图象的应用以及数形结合思想.而函数的零点、方程根的问题也是高考的热点,题型既有选择题、填空题,又有解答题.客观题主要考查相应函数的图象与性质,主观题考查较为综合,在考查函数的零点方程根的基础上,又注重考查函数方程、转化与化归、分类讨论、数形结合的思想方法.【2017年高考复习建议与高考命题预测】由前三年的高考命题形式,图象的辨识与对称性以及利用图象研究函数的性质,方程,不等式的解是高考的热点,多以选择题、填空题的形式出现,属中低档题,主要考查基本初等函数的图象的应用以及数形结合思想.而函数的零点、方程根的问题也是高考的热点,题型既有选择题、填空题,又有解答题.客观题主要考查相应函数的图象与性质,主观题考查较为综合,在考查函数的零点方程根的基础上,又注重考查函数方程、转化与化归、分类讨论、数形结合的思想方法.具体对函数图象的考查,主要包括三个方面,“识图”、“作图”、“用图”,其中包含函数图象的变换(平移、伸缩、对称)以及从已知图象提取信息的能力.对方程的考查,实质是对函数与方程思想的考查.一是借助有关基本初等函数的图象,把方程根的问题转化为求函数图象交点问题,把根的个数问题转化为函数图象交点个数问题;二是通过建立函数关系式,把方程问题转化为讨论函数性质的问题;三是直接解方程.所以函数图象与方程式密不可分的整体,方程问题最终归根于一“算”二“看”,所谓“算”就是通过代数的方程,经过对方程的等价变形,直到得到结果位置;所谓“看”就是数形结合,把根转化为交点问题处理.预测2017年仍然会有函数图象与方程的题目出现,而且会加大...