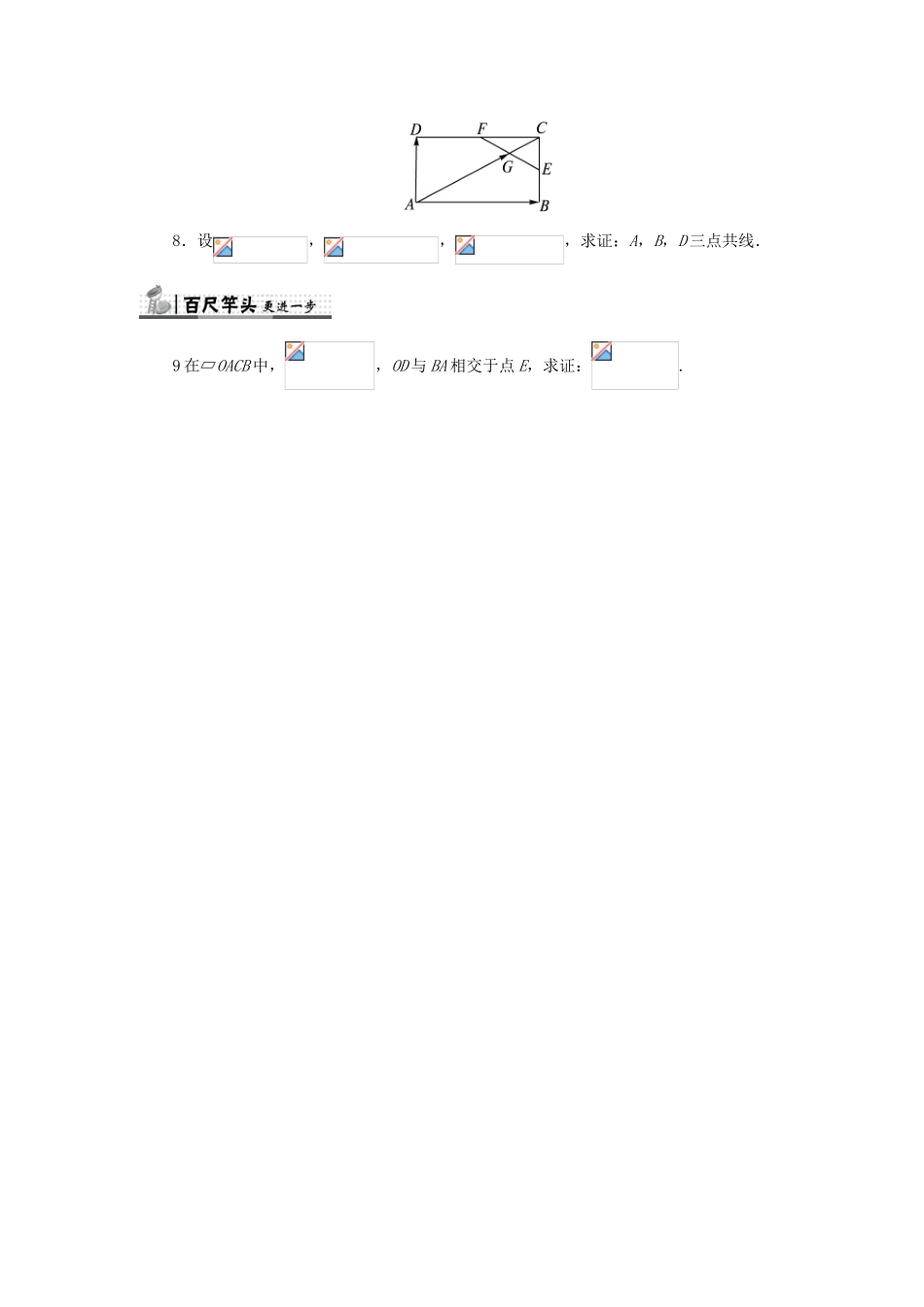
2.3.1平面向量基本定理2.3.2平面向量的正交分解及坐标表示自我小测1.下面三种说法中,正确的是().①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底;②一个平面内有无数多对不共线向量可作为表示该平面所有向量的基底;③零向量不可为基底中的向量.A.①②B.②③C.①③D.①②③2.设O是的对角线交点,下列向量组:①与;②与;③与;④与,其中可作为这个平行四边形所在平面的表示它的所有向量的基底的是().A.①②B.①③C.①④D.③④3.如果e1,e2是平面α内所有向量的一组基底,那么().A.若存在实数λ1,λ2使,则λ1=λ2=0B.空间任一向量a可以表示为a=λ1e1+λ2e2,这里λ1,λ2是实数C.对实数λ1,λ2,λ1e1+λ2e2不一定在平面α内D.对平面α内的任一向量a,使a=λ1e1+λ2e2的实数λ1,λ2有无数组4.若,,,则等于().A.a+λbB.λa+bC.λa+(1+λ)bD.5.已知e1,e2是非零的不共线向量,a=ke1+e2,b=e1+k2e2,且a∥b,则k=__________.6.已知e1,e2不共线,a=e1+2e2,b=2e1+λe2,要使a,b能作为平面内所有向量的一组基底,则实数λ的取值范围是__________.7.如图,已知E,F分别是矩形ABCD的边BC,CD的中点,EF与AC交于点G,若,,用a,b表示.8.设,,,求证:A,B,D三点共线.9在▱OACB中,,OD与BA相交于点E,求证:.参考答案1答案:B解析:由于任意不共线的向量a、b都可以作为基底,故①是错的,而②③是对的,故选B.2答案:B解析:∵与不共线,故可作为平面向量的一组基底,排除D;又,故②不可以作为基底,排除A;与不共线,故③可以,故选B.3答案:A解析:由于e1和e2是平面α内的向量的一组基底,故e1和e2不共线,所以当λ1e1+λ2e2=0时,λ1=λ2=0.故选A.4答案:D解析:由于,故点P在直线P1P2上,∴,∴.∴.故选D.5答案:1解析:由a∥b,则得a=λb,ke1+e2=λ(e1+k2e2),确定关于k,λ的方程组.∵a∥b,a=ke1+e2,b=e1+k2e2,∴a=λb,即ke1+e2=λ(e1+k2e2).∴ke1+e2=λe1+λk2e2.∴∴k3=1.∴k=1.6答案:λ≠4解析:考虑向量a,b共线,则有λ=4,故当向量a,b不共线时,λ≠4.7解:易知,,设,则由平行四边形法则可得,由于E,G,F三点共线,则2λ+2λ=1,即,从而,从而.8解:要证三点A,B,D共线,只要证明中的实数λ存在.由,,,得,即(a+5b)+(-2a+8b)+3(a-b)=λ(a+5b),得2a+10b=λa+5λb.若a与b共线,则显然A,B,D三点共线;若a,b不共线,由平面向量的基本定理有∴λ=2,即,∴A,B,D三点共线.9证明:∵O,E,D三点共线,∴向量与向量共线,则存在实数λ1,使得,而.则.又∵A,E,B三点共线,∴与共线,则存在实数λ2,使.∴.而,∴.即.∵与不共线,∴∴.∴,故.