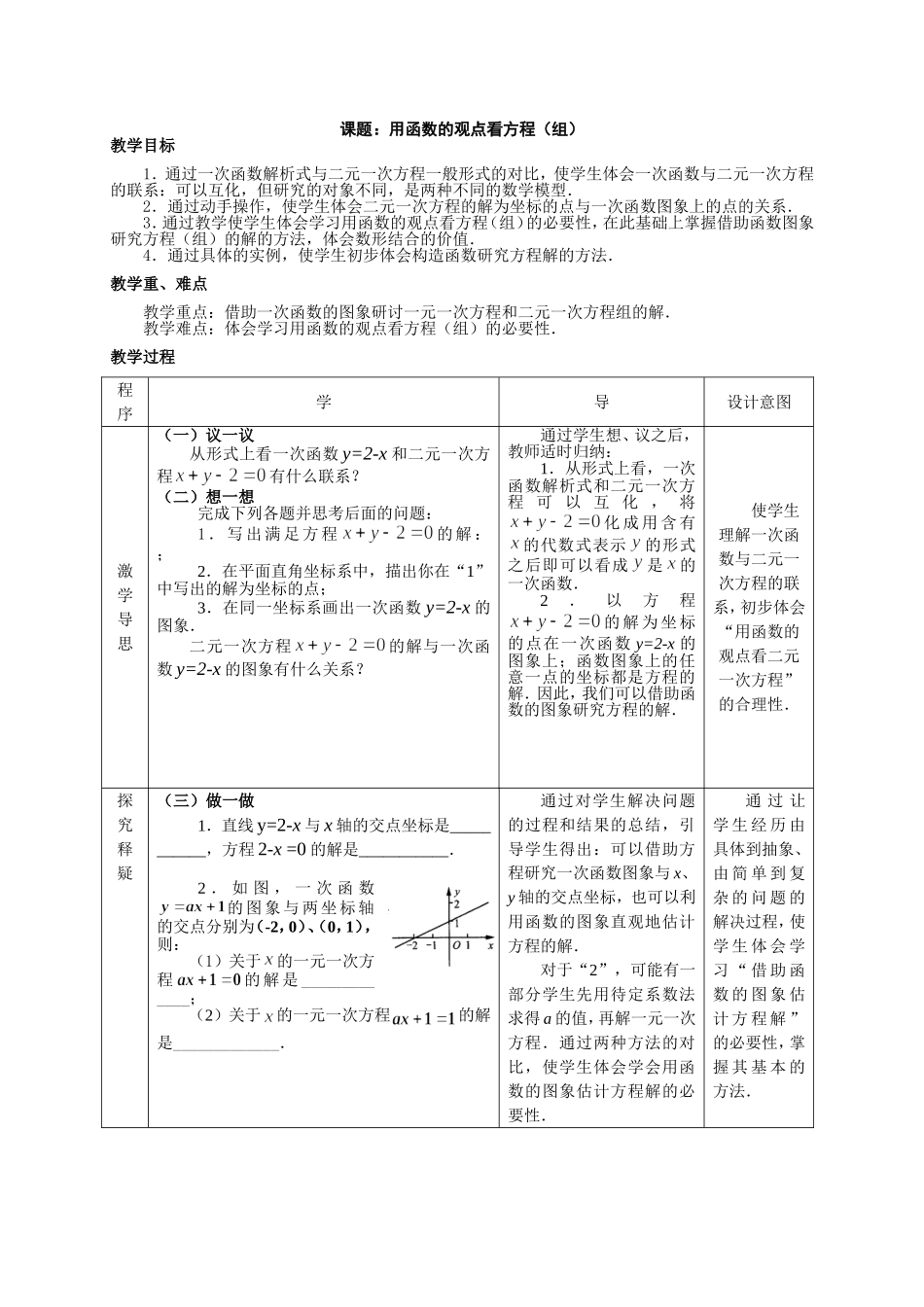
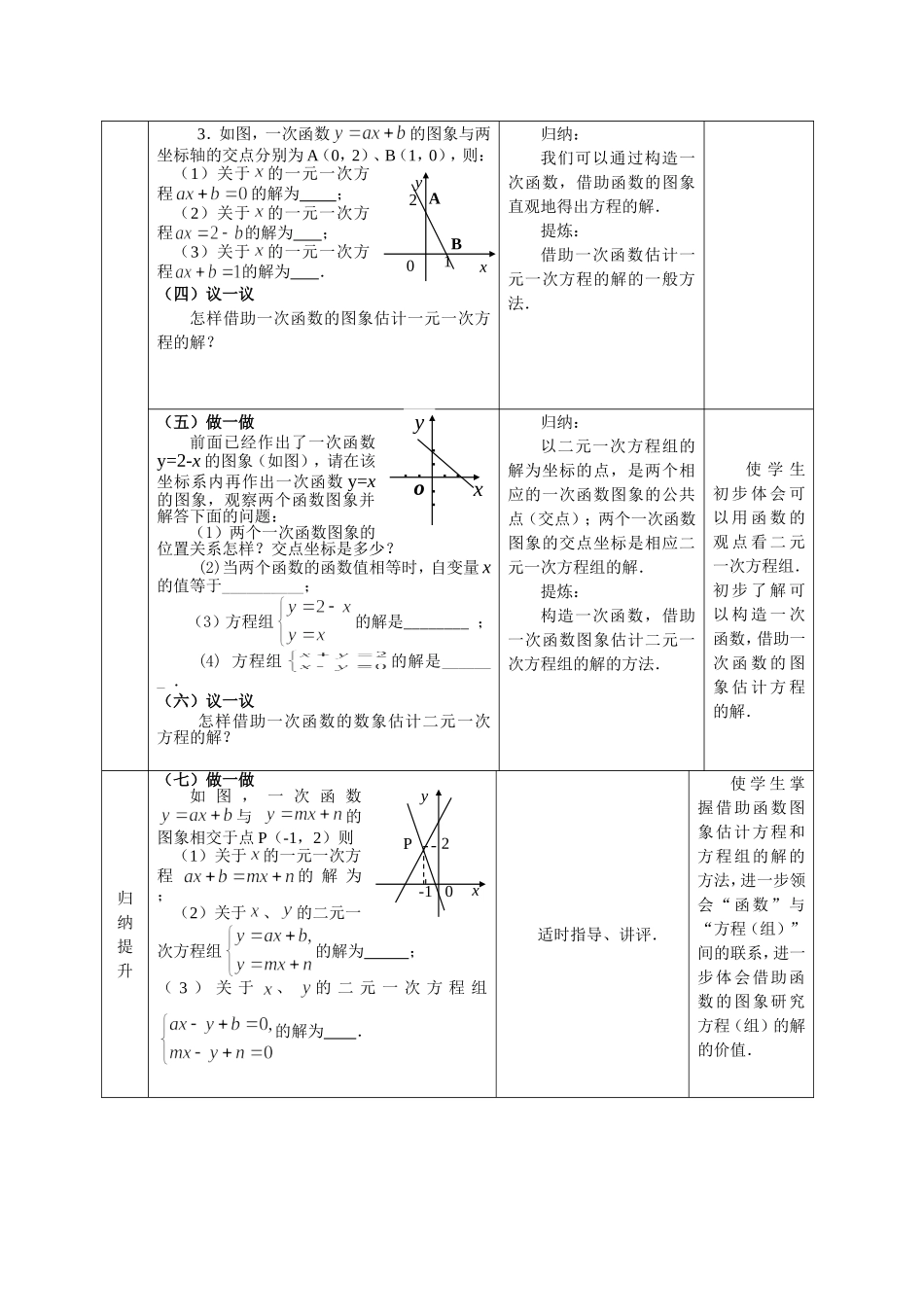
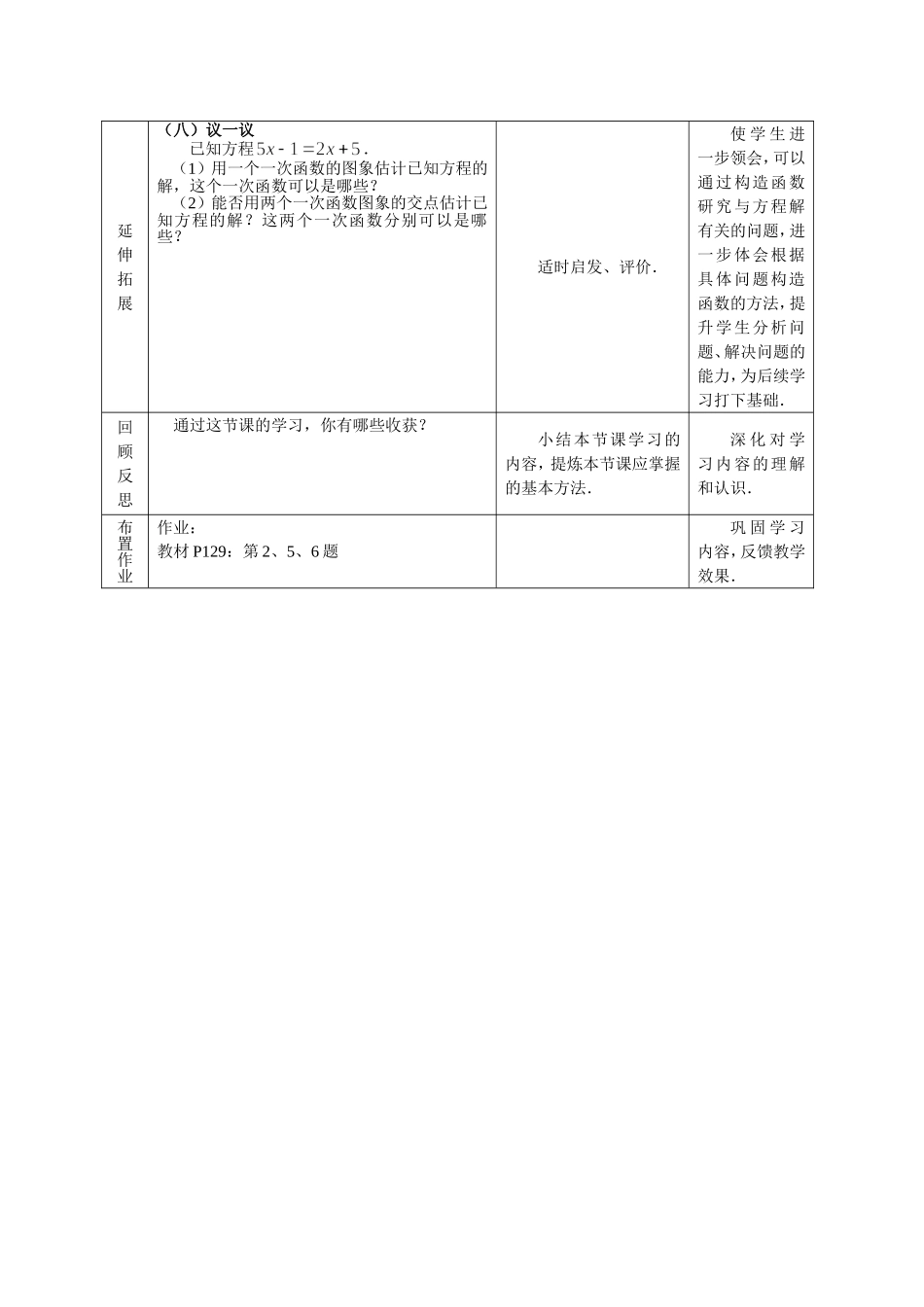
课题:用函数的观点看方程(组)教学目标1.通过一次函数解析式与二元一次方程一般形式的对比,使学生体会一次函数与二元一次方程的联系:可以互化,但研究的对象不同,是两种不同的数学模型.2.通过动手操作,使学生体会二元一次方程的解为坐标的点与一次函数图象上的点的关系.3.通过教学使学生体会学习用函数的观点看方程(组)的必要性,在此基础上掌握借助函数图象研究方程(组)的解的方法,体会数形结合的价值.4.通过具体的实例,使学生初步体会构造函数研究方程解的方法.教学重、难点教学重点:借助一次函数的图象研讨一元一次方程和二元一次方程组的解.教学难点:体会学习用函数的观点看方程(组)的必要性.教学过程程序学导设计意图激学导思(一)议一议从形式上看一次函数y=2-x和二元一次方程有什么联系?(二)想一想完成下列各题并思考后面的问题:1.写出满足方程的解:;2.在平面直角坐标系中,描出你在“1”中写出的解为坐标的点;3.在同一坐标系画出一次函数y=2-x的图象.二元一次方程的解与一次函数y=2-x的图象有什么关系?通过学生想、议之后,教师适时归纳:1.从形式上看,一次函数解析式和二元一次方程可以互化,将化成用含有的代数式表示的形式之后即可以看成是的一次函数.2.以方程的解为坐标的点在一次函数y=2-x的图象上;函数图象上的任意一点的坐标都是方程的解.因此,我们可以借助函数的图象研究方程的解.使学生理解一次函数与二元一次方程的联系,初步体会“用函数的观点看二元一次方程”的合理性.探究释疑(三)做一做1.直线y=2-x与x轴的交点坐标是___________,方程2-x=0的解是___________.2.如图,一次函数的图象与两坐标轴的交点分别为(-2,0)、(0,1),则:(1)关于的一元一次方程的解是_____________;(2)关于的一元一次方程的解是_____________.通过对学生解决问题的过程和结果的总结,引导学生得出:可以借助方程研究一次函数图象与x、y轴的交点坐标,也可以利用函数的图象直观地估计方程的解.对于“2”,可能有一部分学生先用待定系数法求得a的值,再解一元一次方程.通过两种方法的对比,使学生体会学会用函数的图象估计方程解的必要性.通过让学生经历由具体到抽象、由简单到复杂的问题的解决过程,使学生体会学习“借助函数的图象估计方程解”的必要性,掌握其基本的方法.3.如图,一次函数的图象与两坐标轴的交点分别为A(0,2)、B(1,0),则:(1)关于的一元一次方程的解为;(2)关于的一元一次方程的解为;(3)关于的一元一次方程的解为.(四)议一议怎样借助一次函数的图象估计一元一次方程的解?归纳:我们可以通过构造一次函数,借助函数的图象直观地得出方程的解.提炼:借助一次函数估计一元一次方程的解的一般方法.(五)做一做前面已经作出了一次函数y=2-x的图象(如图),请在该坐标系内再作出一次函数y=x的图象,观察两个函数图象并解答下面的问题:(1)两个一次函数图象的位置关系怎样?交点坐标是多少?(2)当两个函数的函数值相等时,自变量x的值等于__________;(3)方程组的解是________;(4)方程组的解是_______.(六)议一议怎样借助一次函数的数象估计二元一次方程的解?归纳:以二元一次方程组的解为坐标的点,是两个相应的一次函数图象的公共点(交点);两个一次函数图象的交点坐标是相应二元一次方程组的解.提炼:构造一次函数,借助一次函数图象估计二元一次方程组的解的方法.使学生初步体会可以用函数的观点看二元一次方程组.初步了解可以构造一次函数,借助一次函数的图象估计方程的解.归纳提升(七)做一做如图,一次函数与的图象相交于点P(-1,2)则(1)关于的一元一次方程的解为;(2)关于、的二元一次方程组的解为;(3)关于、的二元一次方程组的解为.适时指导、讲评.使学生掌握借助函数图象估计方程和方程组的解的方法,进一步领会“函数”与“方程(组)”间的联系,进一步体会借助函数的图象研究方程(组)的解的价值.P0xy-12yoxBA0xy12延伸拓展(八)议一议已知方程.(1)用一个一次函数的图象估计已知方程的解,这个一次函数可以是哪些?(2)能否...