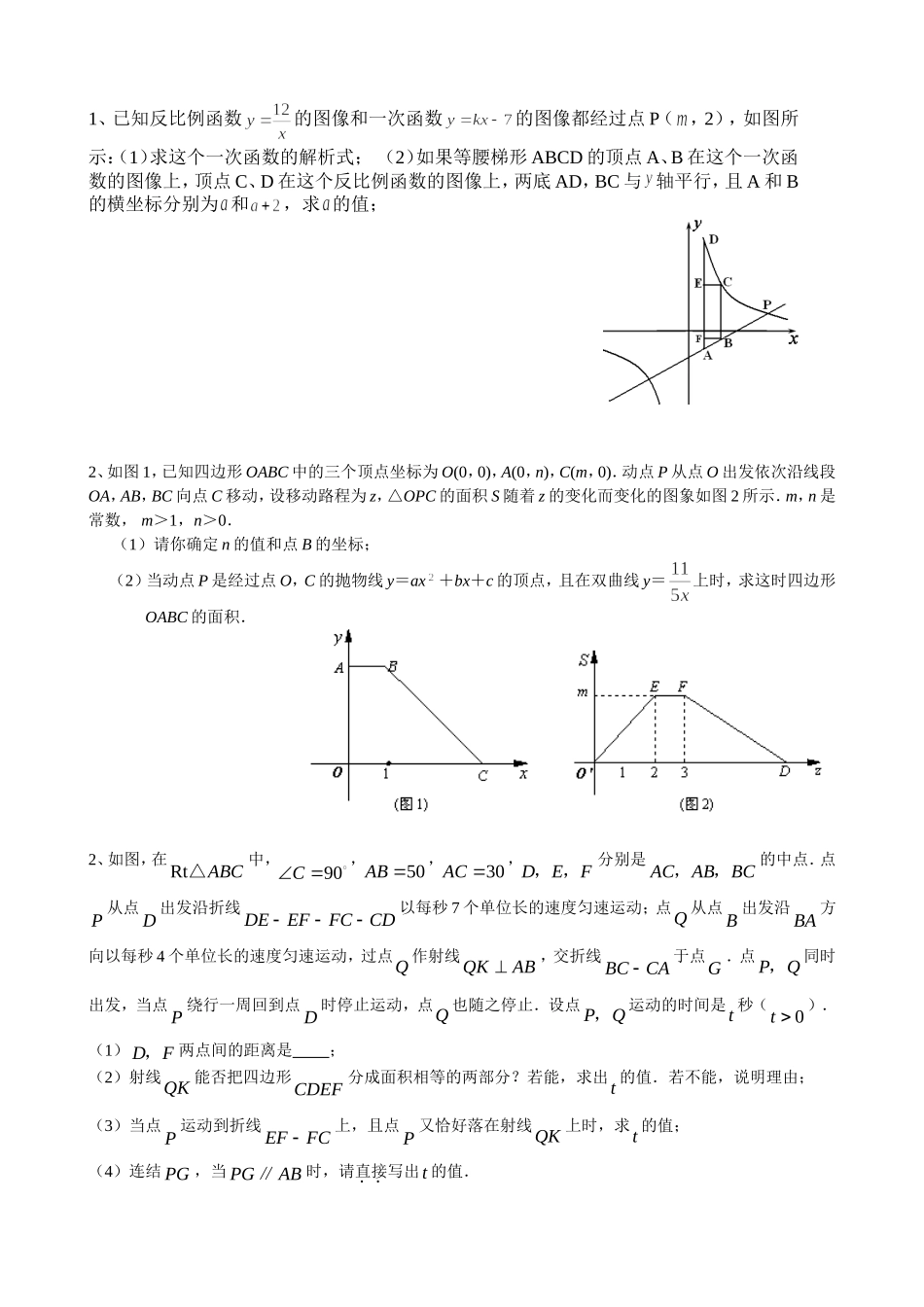
1、已知反比例函数的图像和一次函数的图像都经过点P(,2),如图所示:(1)求这个一次函数的解析式;(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图像上,顶点C、D在这个反比例函数的图像上,两底AD,BC与轴平行,且A和B的横坐标分别为和,求的值;2、如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出发依次沿线段OA,AB,BC向点C移动,设移动路程为z,△OPC的面积S随着z的变化而变化的图象如图2所示.m,n是常数,m>1,n>0.(1)请你确定n的值和点B的坐标;(2)当动点P是经过点O,C的抛物线y=ax+bx+c的顶点,且在双曲线y=上时,求这时四边形OABC的面积.2、如图,在RtABC△中,90C,50AB,30AC,DEF,,分别是ACABBC,,的中点.点P从点D出发沿折线DEEFFCCD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QKAB,交折线BCCA于点G.点PQ,同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点PQ,运动的时间是t秒(0t).(1)DF,两点间的距离是;(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值.若不能,说明理由;(3)当点P运动到折线EFFC上,且点P又恰好落在射线QK上时,求t的值;(4)连结PG,当PGAB∥时,请直接写出t的值.2、如图,二资助函数的图象经过点M(1,)、N(,6);(1)求二次函数的解析式;(2)把Rt△ABC放在坐标系内,其中∠CAB=90°,点A,B的坐标分别为(1,0)、(4,0),BC=5.将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离;22、如图,矩形ABCD中,AD>AB,BD=10,E、F分别是BC、CD上的点,且EC+CF=4,设∠ABD=,∠DBC=,、是关于的方程的两个实数根;(1)求的值;(2)设CE=t,△AEF的面积为S,写出S关于t的函数关系式,并求出△AEF的最小面积;(3)如果BD与AE、AF分别交于M、N,那么M、N能否把BD三等分?如果能,求出此时CE的场;如果不能,请说明理由;5、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13cm,BC=16cm,CD=5cm,AB为⊙O的直径,动点P沿AD方向从点A开始向点D以1cm/s的速度运动,动点Q沿CB方向从点C开始向点B以2cm/s的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.(1)求⊙O的直径;(2)求四边形PQCD的面积y关于P、Q运动时间t的函数关系式,并求四边形PQCD为等腰梯形时,四边形PQCD的面积.(3)是否存在某一时刻t,使直线PQ与⊙O相切,若存在,求出t的值;若不存在,请说明理由.