平面向量数量积VIP免费

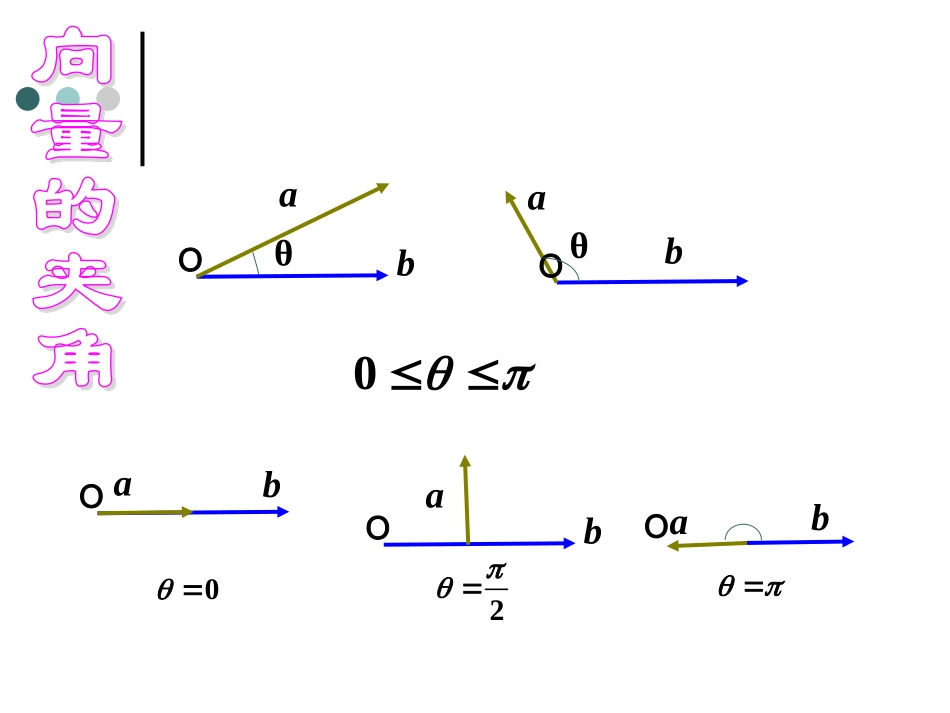
2.4.1平面向量数量积的物理背景及其含义2.4.2平面向量数量积的坐标表示、模、夹角一般地，我们规定实数λ与向量的积是一个向量，这种运算叫做向量的数乘，记作，它的长度和方向规定如下：aa||||||;aa（1）（2）当时，的方向与的方向相同；当时，的方向与的方向相反。aa0aa0特别的，当时，00.a平面向量数量积的定义OθOθ0ababOab0Oab2Oab•问（1）力F所做的功W=。•（２）请同学们分析这个公式的特点：•W（功）是量，•F（力）是量，•S（位移）是量，•θ是量。我们学过功的概念，即一个物体在力F的作用下产生位移s（如图）θFS问题思考|s||F|Wcos标标矢矢探究数量积的含义１、概念的抽象问题4：你能用文字语言来表述功的计算公式吗?如果我们将公式中的力与位移推广到一般向量，其结果又该如何表述？功是力与位移的大小及其夹角余弦值的乘积；结果是两个向量的大小及其夹角余弦值的乘积。从力所做的功出发，我们引入向量“数量积”的概念。平面向量的数量积babababa记作的数量积（或内积），和叫做，我们把数量它们的夹角为和两个非零向量cos,cosbaba即0一向量的数量积为我们规定：零向量与任00a即思考：向量的数量积是一个数量，那么它什么时候为正，什么时候为负？当0°≤θ＜90°时为正；当90°＜θ≤180°时为负。当θ=90°时为零。||||cosababababab时，当反向时，与当同向时，与当bababababababa0baaa2a2a2aaaa或时特别地：当bacosbaba平面向量的数量积：注意!!:平面向量的数量积cosbaba.,,..2注意它们的区别或或的乘法运算可写成而对于两实数”能写成“”不能省略不写，也不中“在书写中babaabbaba则而言，若思考：对于实数,0,abba00ba或?..1向量算结果是数量，而不是两平面向量的数量积运000baba或则那么若,babababa求求：已知例,43)2(;,//)1(2,11，分两种情况：）由解：（ba//1;2,baba同向，当。反向，当2,baba143cos212ba）（解：a·b=|a||b|cosθ=5×4×cos120°=5×4×（-1/2）=－10例2已知|a|=5，|b|=4，a与b的夹角θ=120°，求a·b。θO投影||||cosababOθab||cosbab在上的投影：||cos0bOab||cos0bab||cos0b||cosaba在上的投影：||||cosabba数量积等于与投影的乘积。练习判断下列说法是否正确(×)(√)(×)(×)(√)(√)至少有一个为零向量则若则若有则对任一非零向量若有则对任一向量若bababbaababababa,,0)40,0,0)30,,0)20,,0)1则若,)baba6ba∥则若,)baba5ba∥ABCED练习22-2-123如图,边长为2的等边三角形ABC,点D,E分别是边BC,AC的中点,求ACAB）1BCAB）2BCAC）3ACDE）4DEAD）5二、平面向量的数量积的运算律：数量积的运算律：cbcacbabababaabba))(3()()())(2()1(其中，cba、、是任意三个向量，R注：)()(cbacba则(a+b)·c=ON|c|=(OM+MN)|c|=OM|c|+MN|c|=a·c+b·c.ONMa+bbac向量a、b、a+b在c上的射影的数量分别是OM、MN、ON,证明运算律(3)例3：求证：（1）(a＋b)2＝a2＋2a·b＋b2；（2）(a＋b)·(a－b)＝a2－b2.证明：（1）(a＋b)2＝(a＋b)·(a＋b)＝(a＋b)·a＋(a＋b)·b＝a·a＋b·a＋a·b＋b·b＝a2＋2a·b＋b2.例3：求证：（1）(a＋b)2＝a2＋2a·b＋b2；（2）(a＋b)·(a－b)＝a2－b2.证明：（2）(a＋b)·(a－b)＝(a＋b)·a－(a＋b)·b＝a·a＋b·a－a·b－b·b＝a2－b2.P116例4222||6,||4,b60,,(2)(3),(),||abaabababababab已知与的夹角为，求，||||cos12abab解:22||36aa22||16bb(2)(3)abab226aabb22||||||cos6||aabb72...