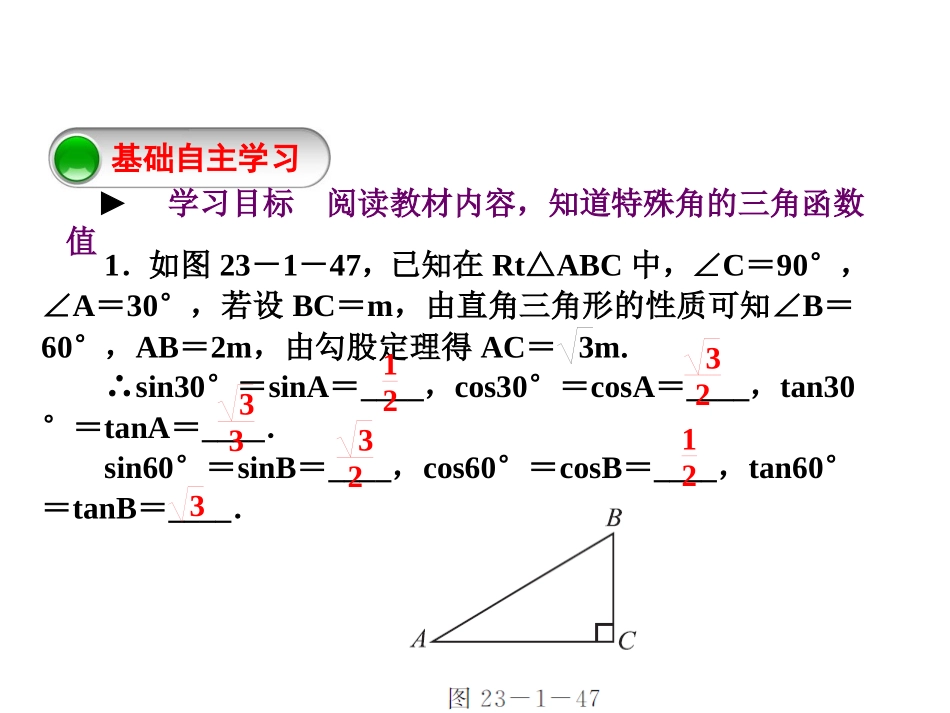
数学新课标(HK)九年级上册基础自主学习基础自主学习重难互动探究重难互动探究课堂小结课堂小结23.1锐角的三角函数第3课时特殊角的三角函数值1.如图23-1-47,已知在Rt△ABC中,∠C=90°,∠A=30°,若设BC=m,由直角三角形的性质可知∠B=60°,AB=2m,由勾股定理得AC=3m.∴sin30°=sinA=____,cos30°=cosA=____,tan30°=tanA=____.sin60°=sinB=____,cos60°=cosB=____,tan60°=tanB=____.基础自主学习►学习目标阅读教材内容,知道特殊角的三角函数值第3课时特殊角的三角函数值12323332123第3课时特殊角的三角函数值2.如图23-1-48,已知在Rt△ABC中,∠C=90°,∠A=45°,若设BC=n,由直角三角形的性质可知∠B=45°,AC=n,由勾股定理得AB=2n.∴sin45°=sinA=____,cos45°=cosA=____,tan45°=tanA=____.22221第3课时特殊角的三角函数值[归纳]特殊角的三角函数值不会随三角形的不同而改变,只要角度确定,那么它的三角函数值就随之确定,根据三角函数定义可知它表示的是直角三角形两边的比,所以要利用三角函数,需要将非直角三角形转化为直角三角形.重难互动探究第3课时特殊角的三角函数值探究问题一会利用特殊角的三角函数值进行计算例1[教材例题变式题]计算:2sin260°-(tan30°)-1×33-2cos245°+(sin30°-2)0.[解析]熟记30°、45°、60°角的三角函数值,了解负指数幂意义a-p=1ap(a≠0),零指数幂意义a0=1(a≠0)即可计算.解:原式=2×(32)2-(33)-1×33-2×(22)2+(12-2)0=2×34-33×33-2×12+1=32-1-1+1=12.探究问题二根据锐角的三角函数特殊值,能说出锐角的度数第3课时特殊角的三角函数值例2在△ABC中,∠A,∠B均为锐角,且有|tanB-3|+(2sinA-3)2=0,则△ABC是()A.直角(不等腰)三角形B.等腰直角三角形C.等腰(非等边)三角形D.等边三角形D第3课时特殊角的三角函数值[解析]因为任何数的绝对值是非负数,任何数的平方是非负数,所以两个非负数相加等于0,则这两个数都等于0.由题意得tanB-3=0,2sinA-3=0,解得tanB=3,sinA=32,故∠A=60°,∠B=60°,利用三角形的内角和定理得∠C=60°,所以△ABC是等边三角形,故选D.[归纳总结]锐角和它的三角函数值是一一对应的关系,已知锐角度数能求出它的三角函数值,反过来,已知它的三角函数值能求出锐角的度数.探究问题三会利用锐角的三角函数特殊值计算三角形的边长第3课时特殊角的三角函数值例3如图23-1-49,△ABC中,∠A=30°,tanB=32,AC=23,求AB的长.[解析]由于△ABC是斜三角形,故作AB边上的高CD,把它转化为直角三角形.在Rt△ADC中,∠A=30°,AC=23,可求出AD和DC的长.在Rt△CDB中,tanB=CDBD=32,而CD已求出,于是可求出BD的长,由AB=AD+BD可求出AB的长.第3课时特殊角的三角函数值解:过点C作CD⊥AB于D,在Rt△ADC中,∵∠A=30°,AC=23,∴CD=AC·sinA=23×sin30°=3,AD=AC·cosA=23·cos30°=3.在Rt△CDB中,tanB=CDBD,BD=CDtanB=332=2.∴AB=AD+BD=3+2=5.[归纳总结]在三角形中已知锐角和一边长,求其他边长时,要构造直角三角形,使已知锐角在直角三角形中,利用特殊角的三角函数值即可确定两边的比值,从而可以解决问题.课堂小结第3课时特殊角的三角函数值____________tanα____________cosα____________sinα60°45°30°角度α三角函数值三角函数1121222223232333第3课时特殊角的三角函数值[反思]特殊角的三角函数值在使用时容易记混,怎样避免呢?下节课将学习它们之间的关系以及三角函数的增减性.[答案]当α为30°,45°,60°时,sinα的值分别为12,22,32,tanα的值分别为33,1,3,由特殊角的三角函数值得sinα<tanα;对于任意的锐角α,在直角三角形中,由正弦、正切的定义可得sinα=α的对边斜边,tanα=α的对边α的邻边.因为邻边(直角边)总是小于斜边,所以sinα<tanα总成立.