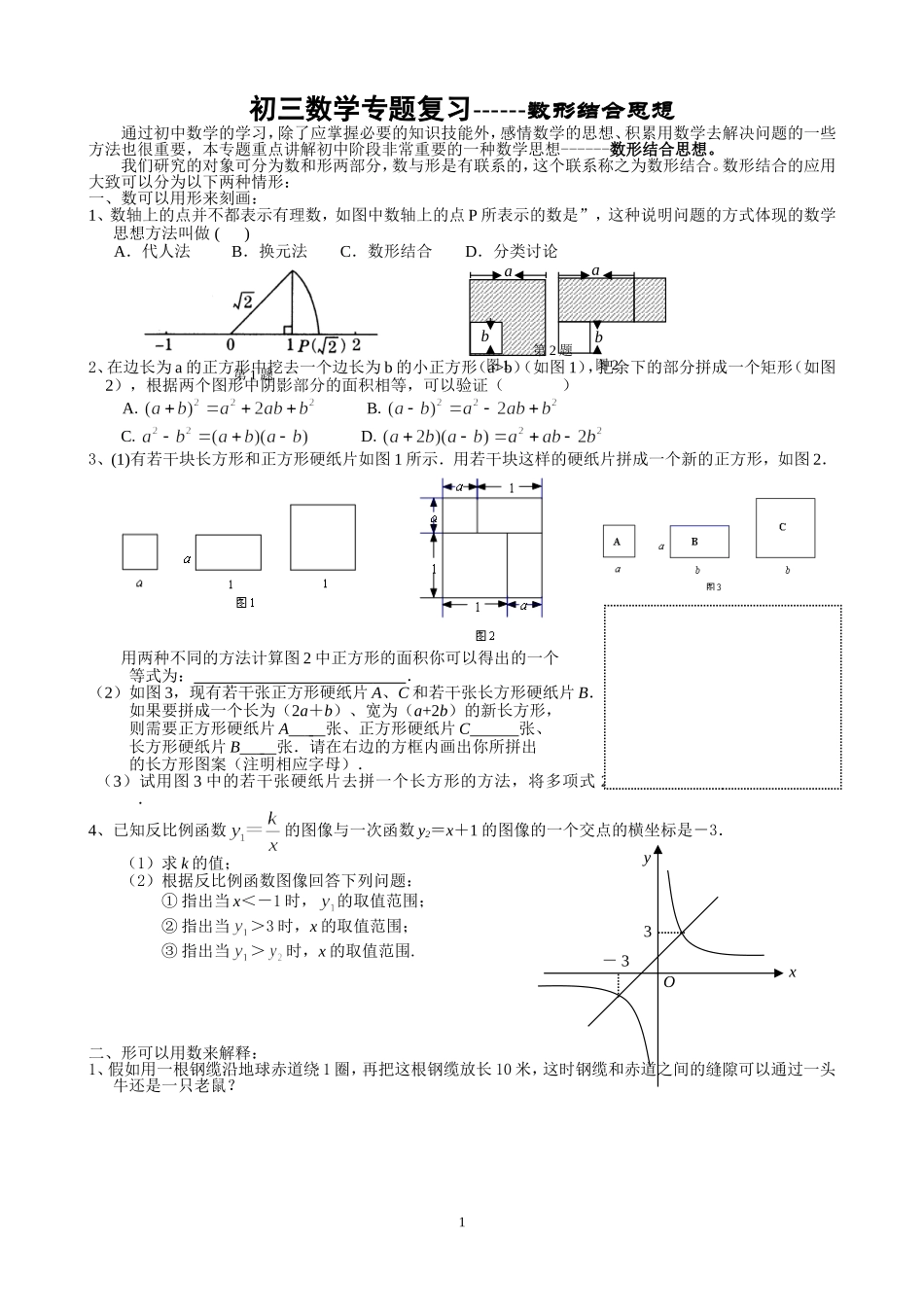
bb图1图2aa初三数学专题复习------数形结合思想通过初中数学的学习,除了应掌握必要的知识技能外,感情数学的思想、积累用数学去解决问题的一些方法也很重要,本专题重点讲解初中阶段非常重要的一种数学思想------数形结合思想。我们研究的对象可分为数和形两部分,数与形是有联系的,这个联系称之为数形结合。数形结合的应用大致可以分为以下两种情形:一、数可以用形来刻画:1、数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想方法叫做()A.代人法B.换元法C.数形结合D.分类讨论2、在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个矩形(如图2),根据两个图形中阴影部分的面积相等,可以验证()A.B.C.D.3、(1)有若干块长方形和正方形硬纸片如图1所示.用若干块这样的硬纸片拼成一个新的正方形,如图2.用两种不同的方法计算图2中正方形的面积你可以得出的一个等式为:.(2)如图3,现有若干张正方形硬纸片A、C和若干张长方形硬纸片B.如果要拼成一个长为(2a+b)、宽为(a+2b)的新长方形,则需要正方形硬纸片A张、正方形硬纸片C张、长方形硬纸片B张.请在右边的方框内画出你所拼出的长方形图案(注明相应字母).(3)试用图3中的若干张硬纸片去拼一个长方形的方法,将多项式2a2+3ab+b2分解因式的结果为.4、已知反比例函数的图像与一次函数y2=x+1的图像的一个交点的横坐标是-3.(1)求k的值;(2)根据反比例函数图像回答下列问题:①指出当x<-1时,的取值范围;②指出当>3时,x的取值范围;③指出当>时,x的取值范围.二、形可以用数来解释:1、假如用一根钢缆沿地球赤道绕1圈,再把这根钢缆放长10米,这时钢缆和赤道之间的缝隙可以通过一头牛还是一只老鼠?1第1题第2题-3xyO32.(3)课堂小结:①你还可以用图形来直观描述初中数学中的某些概念、法则或公式吗?②你还能举一些从数的角度来说明一些图形特征的例子吗?③数可以使形更具有说服力,形可以使数更直观,把形(数)转化为数(形),数形互补,互换获得解决相关问题的思路。课后作业:1.伟伟从学校匀速回家,刚到家发现当晚要完成的试卷忘记在学校,于是马上以更快的速度匀速沿原路返回学校.在这一情景中,速度v和时间t的函数图象(不考虑图象端点情况)大致是()\s\up7()\s\up7()\s\up7()\s\up7()2.文具店、书店和玩具店依次坐落在一条东西走向的大街上,文具店在书店西边20米处,玩具店位于书店2ABCD。东边100米处,小明从书店沿街向东走了40米,接着又向东走了-60米,此时小明的位置在()A.玩具店B.文具店C.文具店西边40米D.玩具店东边-60米3.已知实数a,b在数轴上的对应点依次在原点的右边和左边,那么()A.abbC.a+b>0D.a-b>04.已知函数y=x和y=的图象如图所示,则不等式>x的解集为()A.-2≤x<2B.-2≤x≤2C.x<2D.x>25.如图所示,直线l1∥l2,⊙O与直线l1和直线l2分别相切于点A和点B.点M和点N分别是直线l1和直线l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是()A.MN=B.若MN与⊙O相切,则AM=C.若∠MON=90°,则MN与⊙O相切D.直线l1和直线l2的距离为26.如图,已知四边形OABC为正方形,边长为6,点A、C分别在x轴、y轴的正半轴上,点D在OA上,且点D的坐标为(2,0),点P是OB上的一个动点,则PD+PA的最小值是()A.2B.C.4D.67.“”某电视台走基层栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是()A.汽车在高速公路上的行驶速度为100km/hB.乡村公路总长为90kmC.汽车在乡村公路上的行驶速度为60km/hD.该记者在出发后4.5h到达采访地8.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列结论:①b2-4ac>0;②c<0;③a-b+c>0;④2a+b=0.其中正确的是()A.①②B.②③C.③④D.①④9.张师傅驾车运送荔枝到某地出售,汽车出发前油箱有50升,行驶若干小时后...