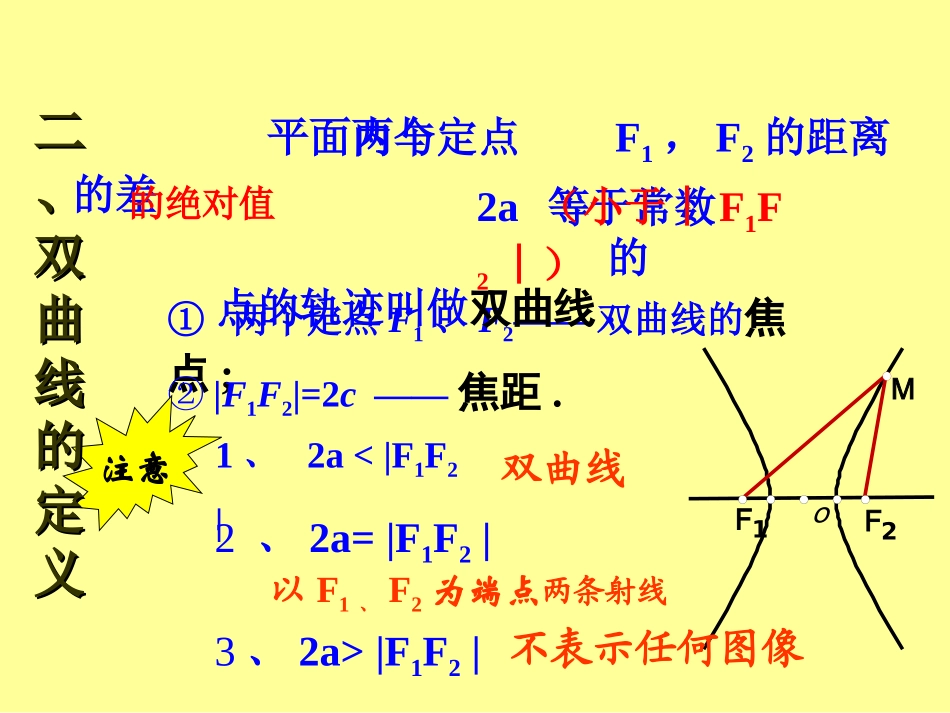
一、复习与回顾1、椭圆的定义2、椭圆的标准方程平面内与两个定点,的距离之和等于常数(大于)的点轨迹叫做椭圆1F2F||21FF12222byax12222bxay或①两个定点F1、F2——双曲线的焦点;②|F1F2|=2c——焦距.oF2F1M平面内与两个定点F1,F2的距离的差等于常数的点的轨迹叫做双曲线.的绝对值2a(小于︱F1F2︱)注意1、2a<|F1F2|双曲线2、2a=|F1F2|以F1、F2为端点两条射线3、2a>|F1F2|不表示任何图像二二、、双双曲曲线线的的定定义义xyo设P(x,y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)常数=2aF1F2P即|(x+c)2+y2-(x-c)2+y2|=2a以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角坐标系1.建系.2.设点.3.列式.|PF1-PF2|=2a4.代点化简.三三、、双双曲曲线线的的标标准准方方程程移项两边平方后整理得:222cxaaxcy两边再平方后整理得:22222222caxayaca由双曲线定义知:22caca220ca设2220cabb代入上式整理得:222210,0xyabab即:三三、、双双曲曲线线的的标标准准方方程程判断下列方程是否表示双曲线,若是,求出其焦点的坐标四四、、标标准准方方程程应应用用124)1(22yx122)2(22yx124)3(22yx3694)4(22xy分析:方程表示双方程表示双曲线时,则曲线时,则mm的取值范围是的取值范围是_________________._________________.11222mymx变式二:21m得0)1)(2(mm由21mm或变式一:如果方程表示双曲线,求的取值范围.11222mymxm四四、、标标准准方方程程应应用用例1、已知双曲线的焦点为F1(-5,0),F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于8,求双曲线的标准方程.∵∵22aa=8,=8,c=5c=5∴∴aa=4,c=5=4,c=5∴∴bb22=5=522--4422=9=9所以所求双曲线的标准方程为:所以所求双曲线的标准方程为:191622yx根据双曲线的焦点在根据双曲线的焦点在xx轴上,设它的标准方程轴上,设它的标准方程为:为:)0,0(12222babyax解:五五、、典典型型例例题题1、已知,是椭圆的两个焦点,平面内一个动点满足则动点的轨迹是()A.双曲线B.双曲线的一个分支C.两条射线D.一条射线1F2FM2||||21MFMFM五五、、典典型型例例题题13422yx2、过双曲线左焦点的直线交双曲线的左支于、两点,为其右焦点,则13422yx1FMN2F___||||||22MNNFMF五五、、典典型型例例题题五五、、典典型型例例题题1.△ABC一边的两个端点是B(0,6)和C(0,-6),另两边所在直线的斜率之积是,求顶点A的轨迹.94小小结结与与作作业业1、双曲线的定义2、双曲线的标准方程及应用3、求解双曲线的方程练习:已知动圆过定点与圆内切,求动圆圆心的轨迹方程.五五、、典典型型例例题题M)0,5(2F36)5(:221yxFM1.若双曲线上的点到点的距离是15,则点到点的距离是()A.7B.23C.5或25D.7或23六六、、走走向向高高考考191622yxP)0,5(P)0,5(2.若椭圆和双曲线有相同的焦点、点为椭圆与双曲线的公共点,则等于()A.B.C.D.六六、、走走向向高高考考122nymx)0(nm122byax)0(ba1F2FP||||21PFPFam)(21am22amam3.设、是双曲线的两个焦点,点在双曲线上,且求的面积______六六、、走走向向高高考考1F2F116922yxP6021PFF21PFF4.设、是双曲线的左、右焦点,若点在双曲线上,且,则()A.B.C.D.1F2F1922yxP021PFPF||||21PFPF10102552