双曲线的简单几何性质(二)VIP免费

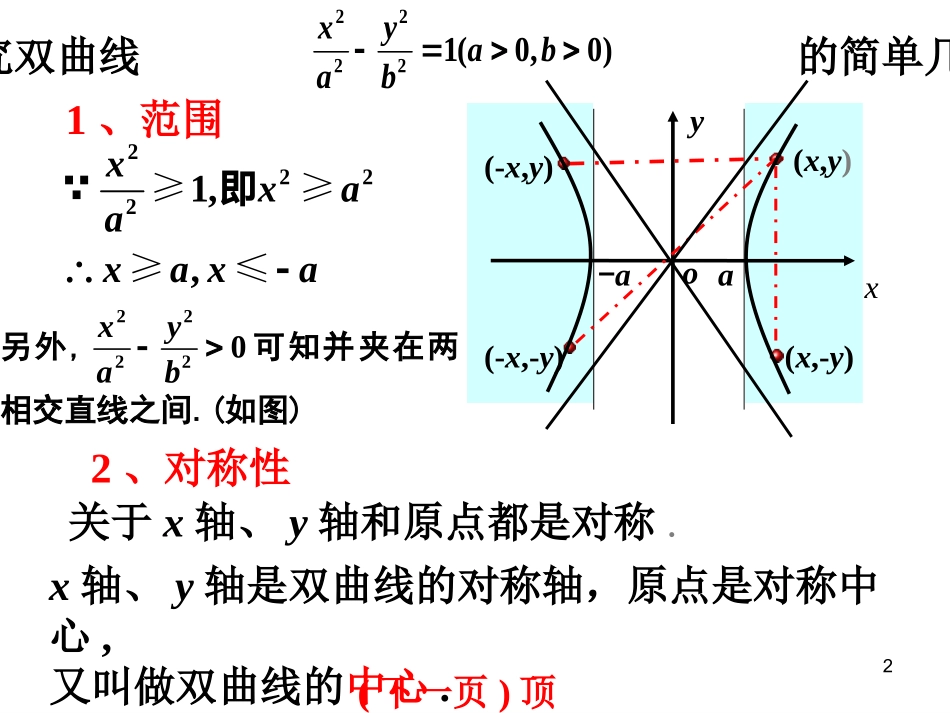
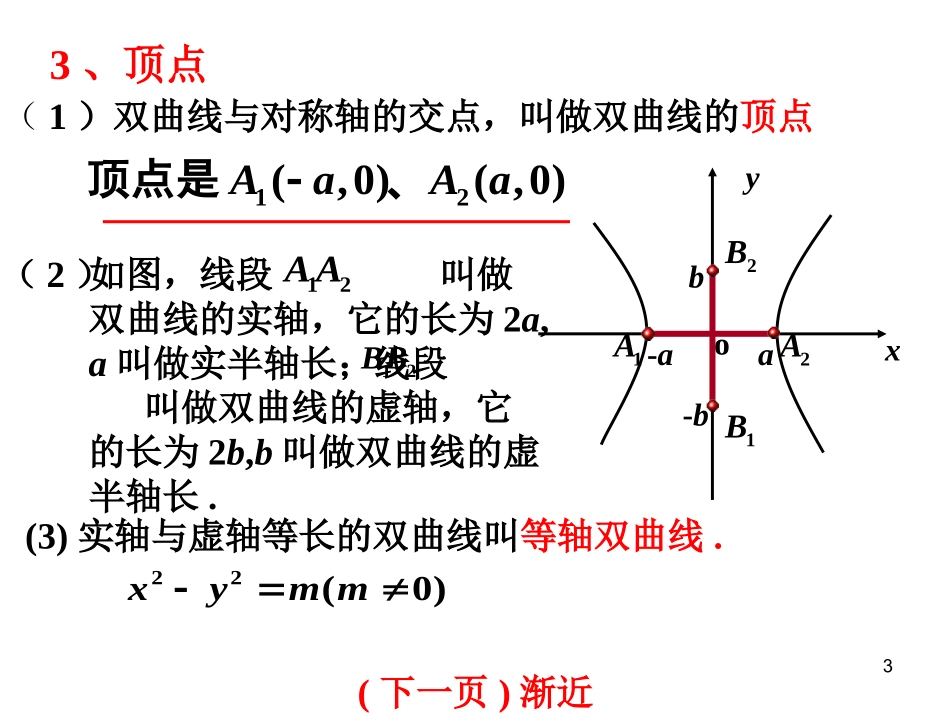
1双曲线的简单几何性质(二)22、对称性一、研究双曲线的简单几何性质1、范围22221,,≥≥≥≤xxaaxaxa即关于x轴、y轴和原点都是对称.x轴、y轴是双曲线的对称轴，原点是对称中心,又叫做双曲线的中心.xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)22221(0,0)xyabab另外,22220xyab可知并夹在两相交直线之间.(如图)(下一页)顶点33、顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点xyo-b1B2Bb1A2A-aa如图，线段叫做双曲线的实轴，它的长为2a,a叫做实半轴长；线段叫做双曲线的虚轴，它的长为2b,b叫做双曲线的虚半轴长.2A1A2B1B（2）(3)实轴与虚轴等长的双曲线叫等轴双曲线.22(0)xymm顶点是12(,0)(,0)AaAa、(下一页)渐近线44、渐近线1A2A1B2Bxyobyxabyxaab利用渐近线可以较准确的画出双曲线的草图(2)渐近线对双曲线的开口的影响(3)动画演示点在双曲线上情况双曲线上的点与这两直线有什么位置关系呢?⑴双曲线22221xyab(0,0)ab的渐近线为byxa注:等轴双曲线22(0)xymm的渐近线为yx(动画演示情况)(下一页)离心率如何记忆双曲线的渐近线方程？55、离心率e是表示双曲线开口大小的一个量,e越大开口越大(动画演示)⑴定义:双曲线的焦距与实轴长的比cea,叫做双曲线的离心率.⑵e的范围:c>a>0e>1⑶e的含义:2222()11bcaceaaa∴当(1,)e时,(0,)ba,且e增大,ba也增大.e增大时,渐近线与实轴的夹角增大.同样可以形象地理解焦点离开中心的程度.另外（4）等轴双曲线的离心率e=?2,反过来也成立. 222,ceabca⑸在、、、abce四个参数中,知二求二.6例1求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐进线方程.可得实半轴长a=4，虚半轴长b=3焦点坐标为（0，-5）、（0，5）45ace离心率xy34渐进线方程为解：把方程化为标准方程221169yx7例2双曲线型自然通风塔的外形，是双曲线的一部分绕其虚轴旋转所成的曲面，它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.选择适当的坐标系，求出此双曲线的方程(精确到1m).A′A0xC′CB′By131225(学习课本例4)8关于x轴、y轴、原点对称图形方程范围对称性顶点离心率1(0)xyabab2222A1（-a，0），A2（a，0）A1（0，-a），A2（0，a）100yx(a,b)ab2222≥≤yayaxR，或关于x轴、y轴、原点对称(1)ceea渐进线ayxb..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c)≥≤xaxayR，或(1)ceeabyxa9例2双曲线型自然通风塔的外形，是双曲线的一部分绕其虚轴旋转所成的曲面，它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.选择适当的坐标系，求出此双曲线的方程(精确到1m).A′A0xC′CB′By131225(学习课本例4)10根据下列条件，求双曲线方程:⑴与双曲线221916xy有共同渐近线，且过点(3,23)；⑵与双曲线221164xy有公共焦点，且过点(32,2)分析:这里所求的双曲线方程易知是标准方程.这里有两种方法来思考:法一:直接设标准方程,运用待定系数法;法二:巧设方程,运用待定系数法.法二可能会比法一简洁,因为设方程思考了.11⑴法一:直接设标准方程,运用待定系数法考虑.(一般要分类讨论)解:双曲线221916xy的渐近线为43yx,令x=-3,y=±4,因234,故点(3,23)在射线43yx（x≤0）及x轴负半轴之间,∴双曲线焦点在x轴上,∴设双曲线方程为22221xyab(a>0,b>0),∴222243(3)(23)1baab解之得22944ab,∴双曲线方程为221944xy根据下列条件，求双曲线方程:⑴与双曲线221916xy有共同渐近线，且过点(3,23)；12法一:直接设标准方程,运用待定系数法⑵解:设双曲线方程为22221xyab(a>0,b>0)则22222220(32)21abab解之得22128ab∴双曲线方程为221128xy根据下列条件，求双曲线方程:⑵与双曲线221164xy有公共焦点，且过点(32,2).13根据下列条件，求双曲线方程:⑴与双曲线221916xy有共同渐近线，且过点(3,23)；⑵与双曲线221164xy有公共焦点，且过点(32,2).法二：巧设方程,运用待定系数法.⑴设双曲线方程为22(0)9...