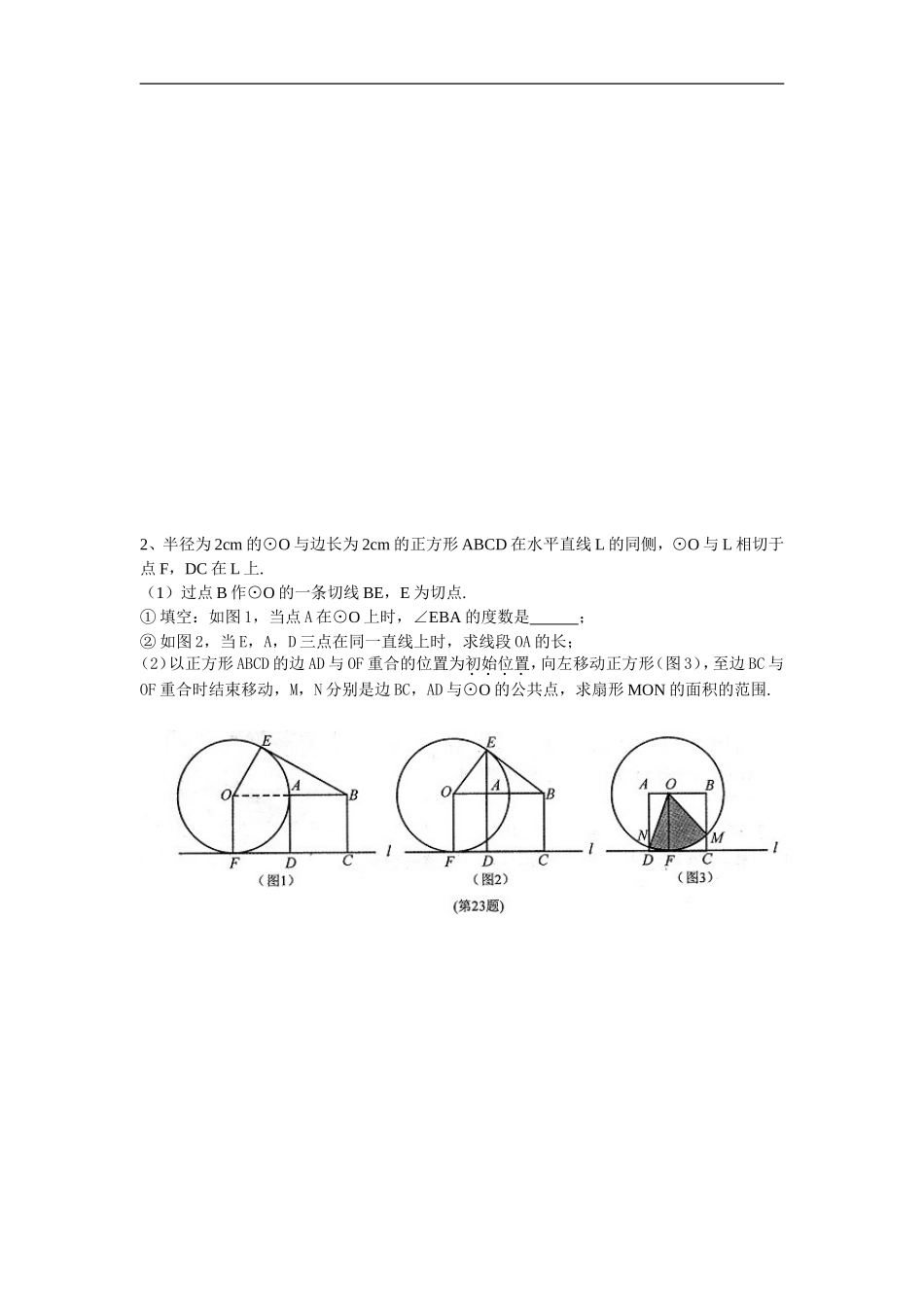
最新初中数学几何综合题1、已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.(1)求证:△ADECDF∽△;(2)当CF:FB=1:2时,求⊙O与▱ABCD的面积之比.解:(1)证明: CD是⊙O的直径,DFC=90°∴∠, 四边形ABCD是平行四边形,A=C∴∠∠,ADBC∥,ADF=DFC=90°∴∠∠,DE 为⊙O的切线,DEDC∴⊥,EDC=90°∴∠,ADF=EDC=90°∴∠∠,ADE=CDF∴∠∠,A=C ∠∠,ADECDE∴△∽△;(2)解: CF:FB=1:2,∴设CF=x,FB=2x,则BC=3x,AE=3EB ,∴设EB=y,则AE=3y,AB=4y, 四边形ABCD是平行四边形,AD=BC=3x∴,AB=DC=4y,ADECDF △∽△,∴=,∴=,x 、y均为正数,x=2y∴,BC=6y∴,CF=2y,在RtDFC△中,∠DFC=90°,由勾股定理得:DF===2y,O∴⊙的面积为π•(DC)2=π•DC2=π(4y)2=4πy2,四边形ABCD的面积为BC•DF=6y•2y=12y2,O∴⊙与四边形ABCD的面积之比为4πy2:12y2=π:3.2、半径为2cm的⊙O与边长为2cm的正方形ABCD在水平直线L的同侧,⊙O与L相切于点F,DC在L上.(1)过点B作⊙O的一条切线BE,E为切点.①填空:如图1,当点A在⊙O上时,∠EBA的度数是;②如图2,当E,A,D三点在同一直线上时,求线段OA的长;(2)以正方形ABCD的边AD与OF重合的位置为初始位置,向左移动正方形(图3),至边BC与OF重合时结束移动,M,N分别是边BC,AD与⊙O的公共点,求扇形MON的面积的范围.解:(1)① 半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,当点A在⊙O上时,过点B作的一条切线BE,E为切点,OB=4∴,EO=2,∠OEB=90°,EBA∴∠的度数是:30°;②如图2, 直线l与⊙O相切于点F,OFD=90°∴∠, 正方形ADCB中,∠ADC=90°,OFAD∴∥,OF=AD=2 ,∴四边形OFDA为平行四边形,OFD=90° ∠,∴平行四边形OFDA为矩形,DAAO∴⊥, 正方形ABCD中,DAAB⊥,O∴,A,B三点在同一条直线上;EAOB∴⊥,OEB=AOE ∠∠,EOABOE∴△∽△,∴=,OE∴2=OA•OB,OA∴(2+OA)=4,解得:OA=1±﹣,OA >0,∴OA=1﹣;方法二:在RtOAE△中,cosEOA=∠=,在RtEOB△中,cosEOB=∠=,∴=,解得:OA=1±﹣,OA >0,∴OA=1﹣;方法三:OEEB ⊥,EAOB⊥,∴由射影定理,得OE2=OA•OB,OA∴(2+OA)=4,解得:OA=1±﹣,OA >0,OA=∴1﹣;(2)如图3,设∠MON=n°,S扇形MON=×22=n(cm2),S随n的增大而增大,∠MON取最大值时,S扇形MON最大,当∠MON取最小值时,S扇形MON最小,过O点作OKMN⊥于K,MON=2NOK∴∠∠,MN=2NK,在RtONK△中,sinNOK=∠=,NOK∴∠随NK的增大而增大,∴∠MON随MN的增大而增大,∴当MN最大时∠MON最大,当MN最小时∠MON最小,①当N,M,A分别与D,B,O重合时,MN最大,MN=BD,MON=BOD=90°∠∠,S扇形MON最大=π(cm2),②当MN=DC=2时,MN最小,ON=MN=OM∴,NOM=60°∴∠,S扇形MON最小=π(cm2),∴π≤S扇形MON≤π.故答案为:30°.3、如图,在直角梯形ABCD中,ADBC∥,∠ABC=90°.点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.(1)点E可以是AD的中点吗?为什么?(2)求证:△ABGBFE∽△;(3)设AD=a,AB=b,BC=c①当四边形EFCD为平行四边形时,求a,b,c应满足的关系;②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.解:(1)不是.据题意得:AE=GE,∠EGB=EAB=90°∠,RtEGD∴△中,GE<ED,AE∴<ED,故,点E不可以是AD的中点;(注:大致说出意思即可;反证法叙述也可)(2)方法一:证明: ADBC∥,AEB=EBF∴∠∠,EABEGB △△≌,AEB=BEG∴∠∠,EBF=BEF∴∠∠,FE=FB∴,FEB∴△为等腰三角形.ABG+GBF=90° ∠∠,∠GBF+EFB=90°∠,ABG=EFB∴∠∠,在等腰△ABG和△FEB中,∠BAG=(180°ABG﹣∠)÷2,FBE=∠(180°EFB﹣∠)÷2,BAG=FBE∴∠∠,…5分ABGBFE∴△∽△,方法二:∠ABG=EFB∠(见方法一),证得两边对应成比例:,由此可得出结论.(3)①方法一: 四边形EFCD为平行四边形,EFDC∴∥,证明两个角相等,得△ABDDCB∽△,∴,即,a∴2+b2=ac;…8分方法二:如图,过点D作DHBC⊥...