4.4--函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用VIP免费

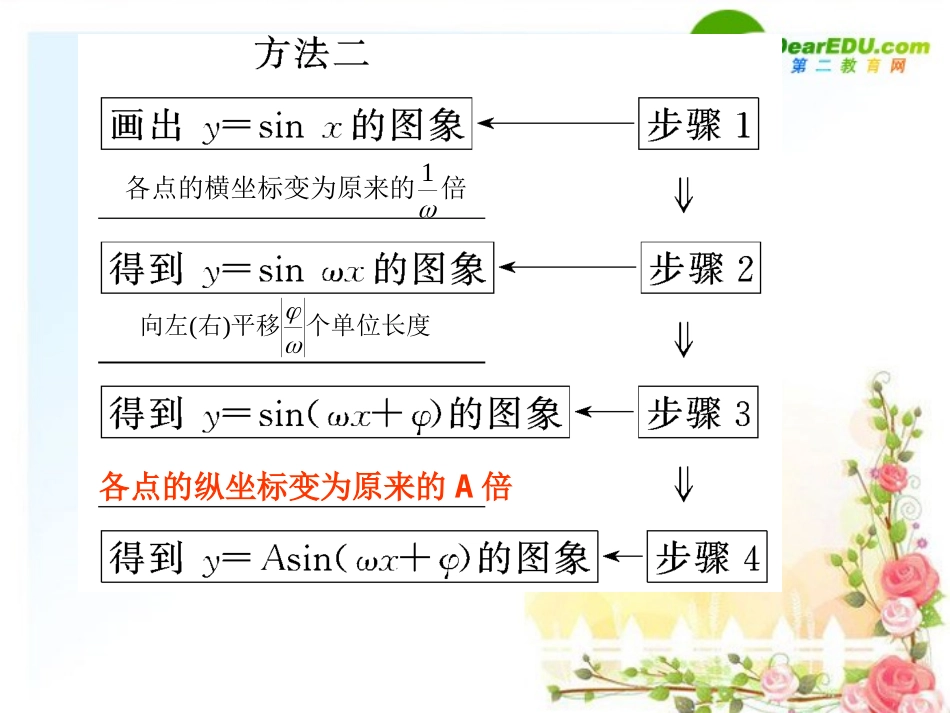
§4.4函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用要点梳理1.用五点法画y=Asin(ωx+φ)一个周期内的简图时，要找五个特征点.如下表所示.x0A0-A002232x02232)sin(xAy基础知识自主学习2.函数y=sinx的图象经变换得到y=Asin(ωx+φ)的图象的步骤如下:个单位长度平移右向左||)(倍的各点的横坐标变为原来1各点的纵坐标变为原来的A倍倍的各点的横坐标变为原来1个单位长度平移右向左)(各点的纵坐标变为原来的A倍以上两种方法的区别:方法一先平移再伸缩;方法二先伸缩再平移.特别注意方法二中的平移量.3.当函数y=Asin(ωx+φ)(A>0,ω>0,x∈(0,+∞))表示一个振动时，A叫做，叫做，叫做，ωx+φ叫做，φ叫做.4.三角函数的图象和性质.振幅2T周期Tf1相位初相频率5.三角函数模型的应用(1)根据图象建立解析式或根据解析式作出图象.(2)将实际问题抽象为与三角函数有关的简单函数模型.(3)利用收集到的数据作出散点图，并根据散点图进行函数拟合，从而得到函数模型.基础自测1.（2009·湖南）将函数y=sinx的图象向左平移φ(0≤φ<2π)个单位后，得到函数的图象，则φ等于（）A.B.C.D.解析将函数y=sinx的图象向左平移φ(0≤φ<2π)个单位得到函数y=sin(x+φ),在A、B、C、D四项中，只有)6sin(xy66567611)611sin(611xy时有).6sin(xD2.为了得到函数x∈R的图象，只需把函数y=2sinx,x∈R的图象上所有的点()A.向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）B.向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）C.向左平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）D.向右平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）),63sin(2xy63163166解析将y=2sinx的图象向左平移个单位得到y=2sin的图象，将y=2sin图象上各点横坐标变为原来的3倍（纵坐标不变），则得到的图象，故选C.答案C6)6(x)6(x)631sin(2xy3.已知函数f(x)=asinx-bcosx(a、b为常数，a≠0,x∈R)在处取得最小值，则函数A.偶函数且它的图象关于点（π，0）对称B.偶函数且它的图象关于点对称C.奇函数且它的图象关于点对称D.奇函数且它的图象关于点（π，0）对称4πx是)4π3(xfy())0,2π3()0,2π3(解析据题意，当时，函数取得最小值，由三角函数的图象与性质可知其图象必关于直线对称，故必有故原函数f(x)=asinx+acosx=4πx4πx,)2π()0(baff),4πsin(2xa.)(π,sin2)4π3(对称点易知其为奇函数且关于从而xaxf答案D,04.将函数y=sin4x的图象向左平移个单位，得到y=sin(4x+φ)的图象，则φ等于（）A.B.C.D.解析将函数y=sin4x的图象向左平移个单位后得到的图象的解析式为1212331212)12(4sinxy.3),34sin(则xC5.（2008·浙江）在同一平面直角坐标系中，函数的图象和直线的交点个数是（）A.0B.1C.2D.4解析函数图象如图所示，直线与该图象有两个交点.])2,0[)(232cos(xxy21y]2,0[,2sin)232cos(xxxy21yC题型一作y=Asin(ωx+φ)的图象已知函数(1)求它的振幅、周期、初相；(2)用“五点法”作出它在一个周期内的图象；(3)说明的图象可由y=sinx的图象经过怎样的变换而得到.(1)由振幅、周期、初相的定义即可解决.(2)五点法作图，关键是找出与x相对应的五个点.(3)只要看清由谁变换得到谁即可.【例1】),32sin(2xy)32sin(2xy思维启迪题型分类深度剖析解（1）的振幅A=2,周期)32sin(2xy,22T.3初相:,.sin2)32sin(2,32)2(并描点画出图象列表则令XxyxXXX方法一把y=sinx的图象上所有的点向左平移个单位,得到的图象,再把的图象上的点的横坐标缩短到原来的倍(纵坐标不变),得到的图象,最后把上所有点的纵坐标伸长到原来的2倍（横坐标不变），即可得到的图象.3)3sin(xy)3sin(xy21)32sin(xy)32sin(xy)32sin(2xy方法二将y=sinx的图象上每一点的横坐标x缩...