经典空几小结夹角距离VIP免费

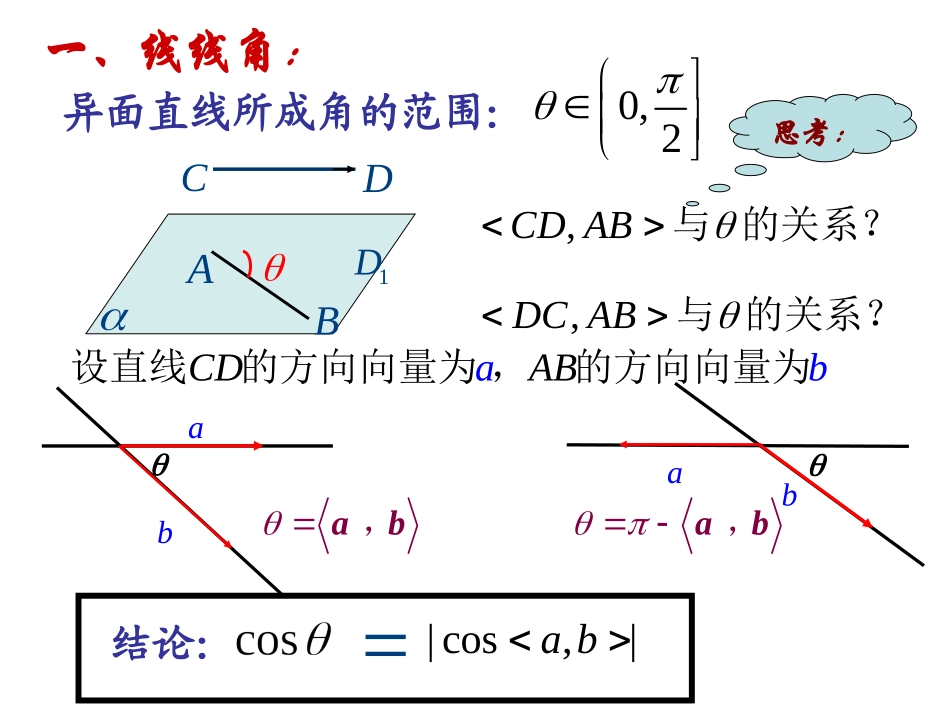
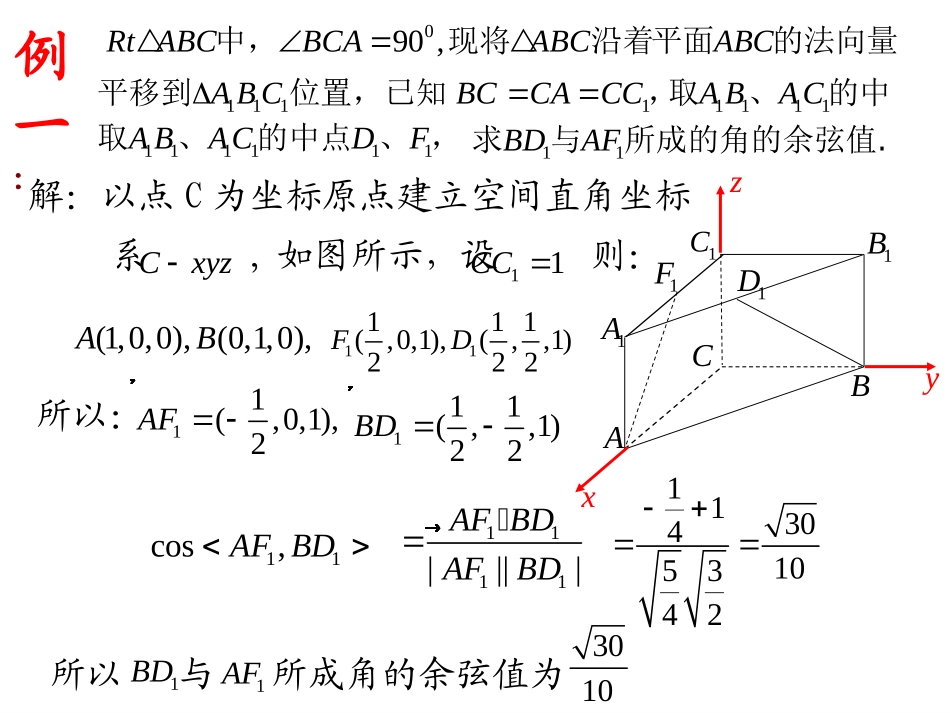
异面直线所成角的范围：0,2ABCD1D,�与的关系？CDAB思考：,�与的关系？DCAB结论：|cos,|ab||一、线线角：ab，ab，设直线的方向向量为，的方向向量为CAaBbDaabb所以与所成角的余弦值为A1AB1BC1C1D1Fxyz解：以点C为坐标原点建立空间直角坐标系,如图所示，设则：Cxyz11CC(1,0,0),(0,1,0),AB11111(,0,1),(,,1)222FD所以：11(,0,1),2�AF111(,,1)22�BD11cos,�AFBD1111||||��AFBDAFBD113041053421BD1AF3010例一：090,中，现将沿着RtABCBCAABC平面的法向量ABC1，BCCACC11求与所成的角的余弦值.BDAF111平移到位置，已知ABC1111取、的中ABAC111111取、的中点、，ABACDF练习：在长方体中，1111ABCDABCD58,ABAD=，14,AA1112,为上的一点,且MBCBM1点在线段上，NAD1.ADAN1.ADAM(1)求证：ABCD1A1B1C1DMNxyz(0,0,0),A(5,2,4),�AM1(0,8,4),�AD10AMAD�＝1.ADAMADANM（2）求与平面所成的角.1(0,0,4),A(0,8,0),D(5,2,4)M简解：例2：1111ABCDABCD的棱长为1.111.BCABC求与面所成的角正方体ABCD1A1B1C1Dxyz2nBA��，直线与平面所成角的范围：[0,]2ABO,��设平面的法向量为，则与的关系？nnBA思考：结论：sin|cos,|��nAB二、线面角：nnBAAB2nBA��，例3：1111ABCDABCD的棱长为1.111.BCABC求与面所成的角正方体ABCD1A1B1C1Dxyz(000)A，，，1(101)B，，，(110)C，，，设正方体棱长为1，1ABADAA�，，为单以1(101)(110)ABAC�，，，，，1(111)C，，，11(010)BC�则，，，1()ABCnxyz设为，，平面的法向量100nABnAC��则，0=10==-1xzxyn=(1-1-1)，，，，，，xyz所以取得故位正交基底，可得110103313cos�，nBC111BCABC3所成的角的正弦值所与面为以3。三.两平面间夹角：ll1n�1n�2n�2n�一进一出于二面角，二面角等于法向量的夹角；左边图同进同出于二面角，二面角等于法向量夹角的补角右边图cos12cos,�nncos12cos,�nn120,0,2平面角中其中范围在内的在两个平面所成的二面角的，称为这两个平面那个角的夹角。两平面间夹角的范围：0,21l2lll三、两平面夹角：①法向量法1n�1n�2n�2n�12nn�，12nn�，12nn�，12nn�，cos12cos,�nncos12cos,�nn注意法向量的方向相对于二面角：一进一出，二面角等于法向量夹角；同进同出，二面角等于法向量夹角的补角1212||cos(||||nnnn��综上：其值大于或等于零）小结：2112nn��和设平面的法向量分别为，若两个平面的夹角为和，则120,2nn�1当时，12=,nn�，121212coscos,=此时：nnnnnn����12,2nn�2当时，12=,,nn�12121212coscos-,=cosn,=此时：nnnnnnn���两平面间夹角的计算过正方形ABCD的顶点A引SA⊥底面ABCD，并使平面SBC，SCD都与底面ABCD成45度角，(1)求两平面夹角B—SC—D的大小？(2)求面SCD与面SAB所夹角大小ABCDSOE060045法向量法！A(0,0,0),C(1,1,0),1,0),D(0,(0,0,1)S1(0,1,0)SBAnAD��易知面的法向量(1,0,0),(0,1,1)CDSD�2(,,),�SCDnxyz的法向量22,,�nCDnSD由得：设平面00xyz2(0,1,1)n�任取1212122cos,2||||nnnnnn���4即所求两平面夹角为[(),,]1OAABADSAAS�：设，建立空间直角坐标系,ABCDS解(2)：以题意可得00,,BASAB=90SBA=45SAlcoscos,ABCDABCDABCD���DCBA四：二面角：ll1n�1n�2n�2n�一进一出于二面角，二面角等于法向量的夹角；左边图同进同出于二面角，二面角等于法向量夹角的补角右边图cos12cos,�nncos12cos,�nn对于这类面面问题，看清楚问...