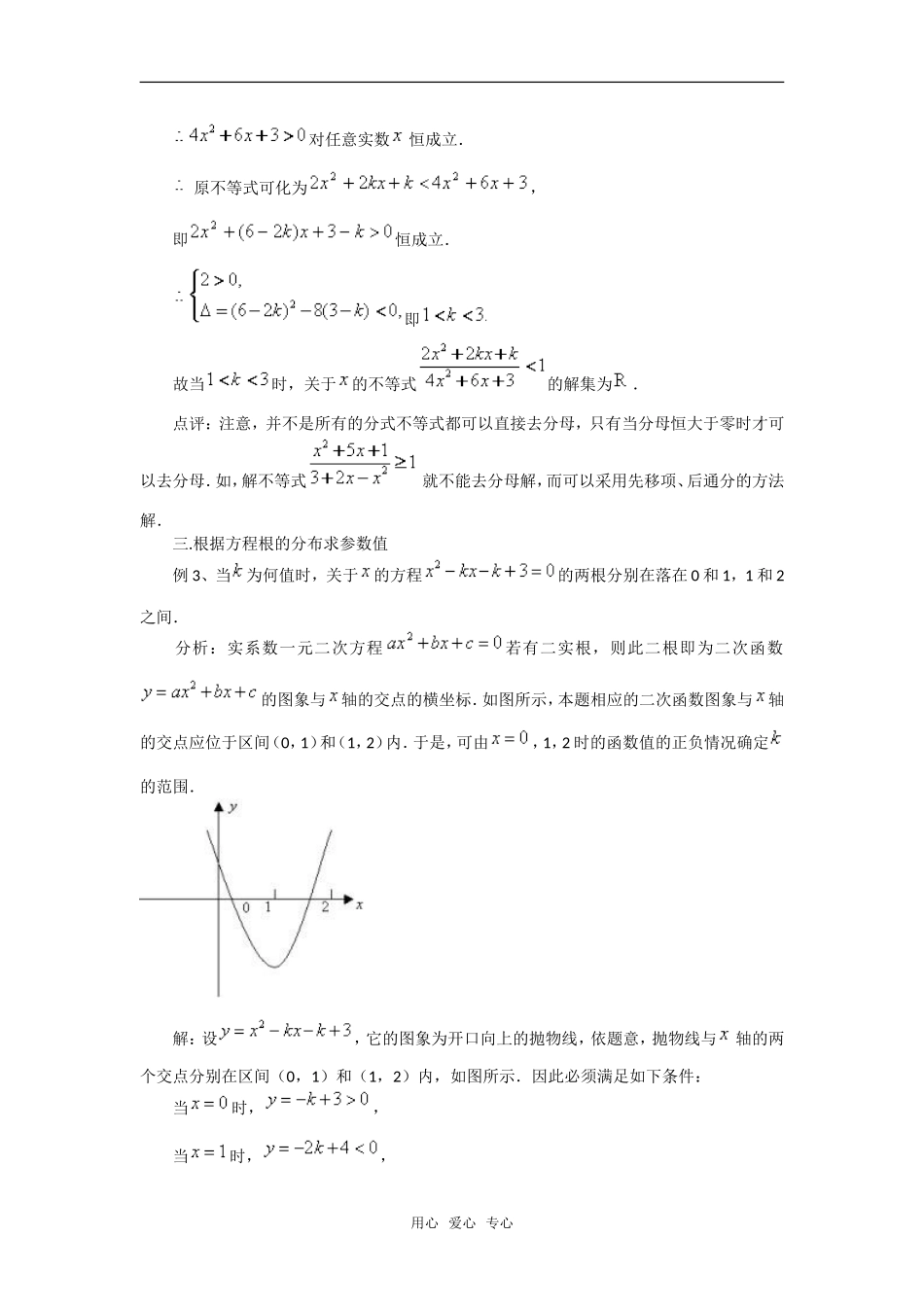
根据二次不等式的解集确定系数例1、已知不等式的解集为,求、的值.分析:此不等式带有两个字母,但不是求解集,而是给出了解集,求字母的值.这就需要逆向思维,根据解集来找相对应的二次方程的解,结合二次函数的图象判断二次项系数的符号等等.解:方法一:显然,由,得,变形得,所以方法二:与是方程的两根,故有,解得(此处注意韦达定理的应用).点评:由二次函数的图象可知,当时,,即抛物线的开口向下,且与轴两交点的横坐标是和,也就是说一元二次方程的两个根为,,因此由方程根与系数的关系可求出的值.显然,二次不等式的解集是由二次函数结合二次方程求得;反之,也可由二次不等式的解集确定二次函数图象和二次方程的实根,本题的求解过程,正是根据三者之间的内在联系.二.分式高次不等式确定参数值例2、为何值时,关于的不等式的解集是一切实数.分析:由于分母的,所以恒成立.故可以在这个不等式的两边同乘以,不等号方向不变.解:分母的,用心爱心专心对任意实数恒成立.原不等式可化为,即恒成立.即故当时,关于的不等式的解集为.点评:注意,并不是所有的分式不等式都可以直接去分母,只有当分母恒大于零时才可以去分母.如,解不等式就不能去分母解,而可以采用先移项、后通分的方法解.三.根据方程根的分布求参数值例3、当为何值时,关于的方程的两根分别在落在0和1,1和2之间.分析:实系数一元二次方程若有二实根,则此二根即为二次函数的图象与轴的交点的横坐标.如图所示,本题相应的二次函数图象与轴的交点应位于区间(0,1)和(1,2)内.于是,可由,1,2时的函数值的正负情况确定的范围.解:设,它的图象为开口向上的抛物线,依题意,抛物线与轴的两个交点分别在区间(0,1)和(1,2)内,如图所示.因此必须满足如下条件:当时,,当时,,用心爱心专心当时,,即解此不等式组得所以当时,方程的两根分别在区间(0,1)和(1,2)内.点评:此题涉及到利用函数图象来判断在特殊值的符号,要让学生注意到在根的两侧的函数值符号相反.四.根据交集求参数例4、已知,且,(),求实数p的取值范围.分析:可以将集合问题转化为根的分布问题,集合A中的方程的根为非正数.解:由知,关于的二次方程无正根.(1)若方程无实根:,得;(2)若方程有实根,,但无正根;此时由,得或,而由韦达定理由知两根均为正或均为负,由条件显然须,,于是,∴因此由上述的(1),(2)得的取值范围是点评:要注意的可能性,否则会“缩小”解的范围,特别对于的存在,初学者往往容易忽略.用心爱心专心