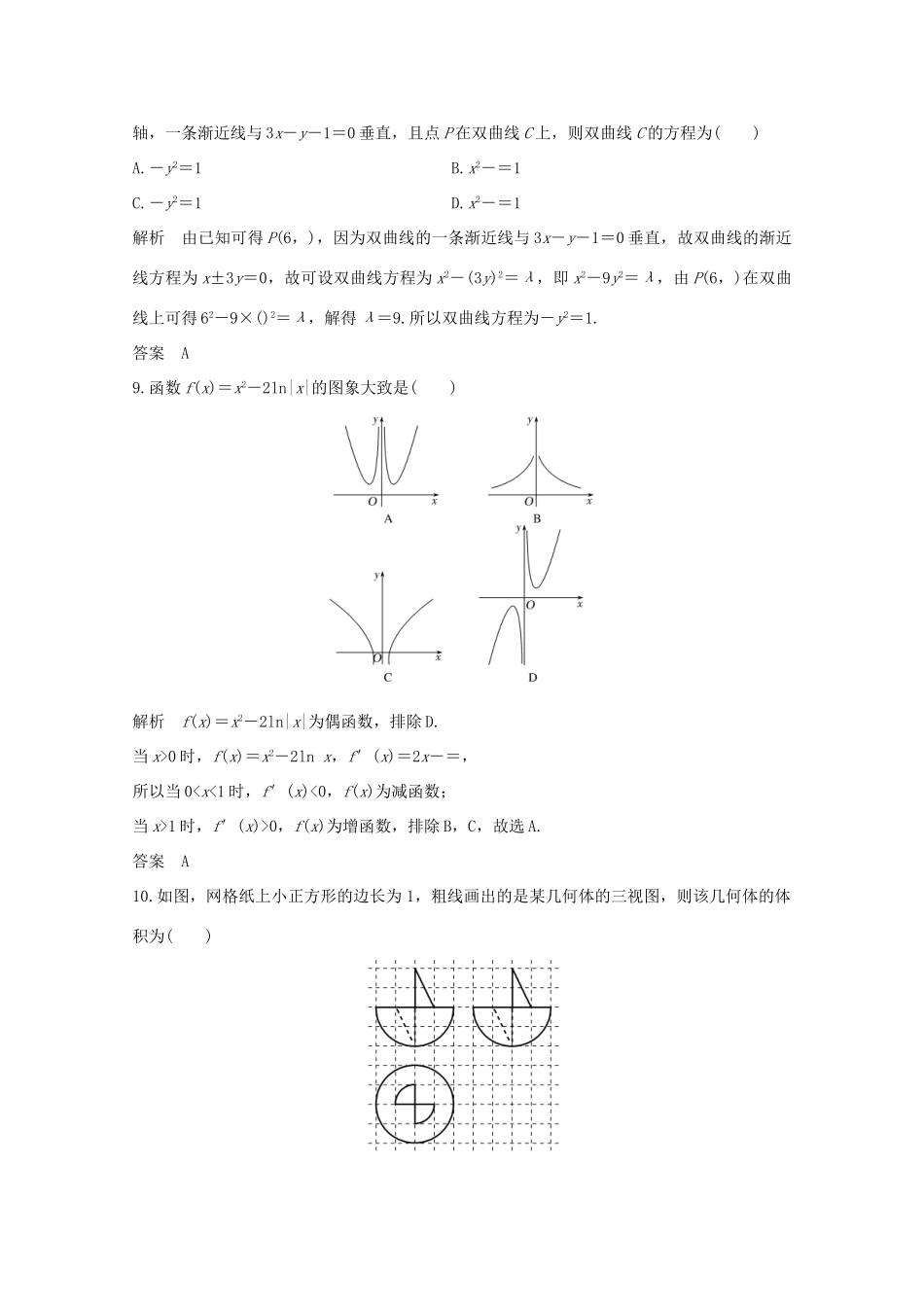
高分突破复习:小题满分限时练(一)(限时:45分钟)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合A={x|x2-6x+8<0},B={x∈N|y=},则A∩B=()A.{3}B.{1,3}C.{1,2}D.{1,2,3}解析由x2-6x+8<0得2n,输出s=29.答案C7.如图,半径为R的圆O内有四个半径相等的小圆,其圆心分别为A,B,C,D,这四个小圆都与圆O内切,且相邻两小圆外切,则在圆O内任取一点,该点恰好取自阴影部分的概率为()A.3-2B.6-4C.9-6D.12-8解析由题意,A,O,C三点共线,且AB⊥BC.设四个小圆的半径为r,则AC=,∴2R-2r=2r,∴R=(+1)r.所以,该点恰好取自阴影部分的概率P===12-8.答案D8.已知函数f(x)=+loga(7-x)(a>0,a≠1)的图象恒过点P,若双曲线C的对称轴为两坐标轴,一条渐近线与3x-y-1=0垂直,且点P在双曲线C上,则双曲线C的方程为()A.-y2=1B.x2-=1C.-y2=1D.x2-=1解析由已知可得P(6,),因为双曲线的一条渐近线与3x-y-1=0垂直,故双曲线的渐近线方程为x±3y=0,故可设双曲线方程为x2-(3y)2=λ,即x2-9y2=λ,由P(6,)在双曲线上可得62-9×()2=λ,解得λ=9.所以双曲线方程为-y2=1.答案A9.函数f(x)=x2-2ln|x|的图象大致是()解析f(x)=x2-2ln|x|为偶函数,排除D.当x>0时,f(x)=x2-2lnx,f′(x)=2x-=,所以当01时,f′(x)>0,f(x)为增函数,排除B,C,故选A.答案A10.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A.πB.πC.πD.π解析该几何体可以看成是在一个半球上叠加一个圆锥,然后挖掉一个相同的圆锥,所以该几何体的体积和半球的体积相等.由图可知,球的半径为2,则V=πr3=.答案A11.将函数f(x)=4sin2x的图象向右平移φ个单位长度后得到函数g(x)的图象,若对于满足|f(x1)-g(x2)|=8的x1,x2,有|x1-x2|min=,则φ=()A.B.C.D.解析由题意知,g(x)=4sin(2x-2φ),满足|f(x1)-g(x2)|=8,不妨设此时x1,x2分别是函数f(x)和g(x)的最小值点和最大值点.即f(x1)=-4,g(x2)=4.则x1=+k1π(k1∈Z),x2=+k2π(k2∈Z),|x1-x2|=(k1,k2∈Z).又|x1-x2|min=,0<φ<,所以φ=.答案C12.已知函数f(x)=ax3+bx2+cx+d在R上是单调递增函数,则的最小值是()A.1B.2C.3D.4解析依题意,f′(x)=3ax2+2bx+c≥0在x∈R恒成立.∴a>0,且Δ=4b2-12ac≤0,则b2≤3ac,c≥>0.又a0,则3a(2b-3a)≤=b2,故≥≥=1.答案A二、填空题(本大题共4个小题,每小题5分,共20分.请把正确的答案填写在各小题的横线上.)13.一个总体分为A,B两层,其个体数之比为5∶1,用分层抽样方法从总体中抽取一个容量为12的样本,已知B层中甲、乙都被抽到的概率为,则总体中的个数为________.解析由条件易知B层中抽取的样本数是2,设B层总体数是n,则又由B层中甲、乙都被抽到的概率是=,可得...