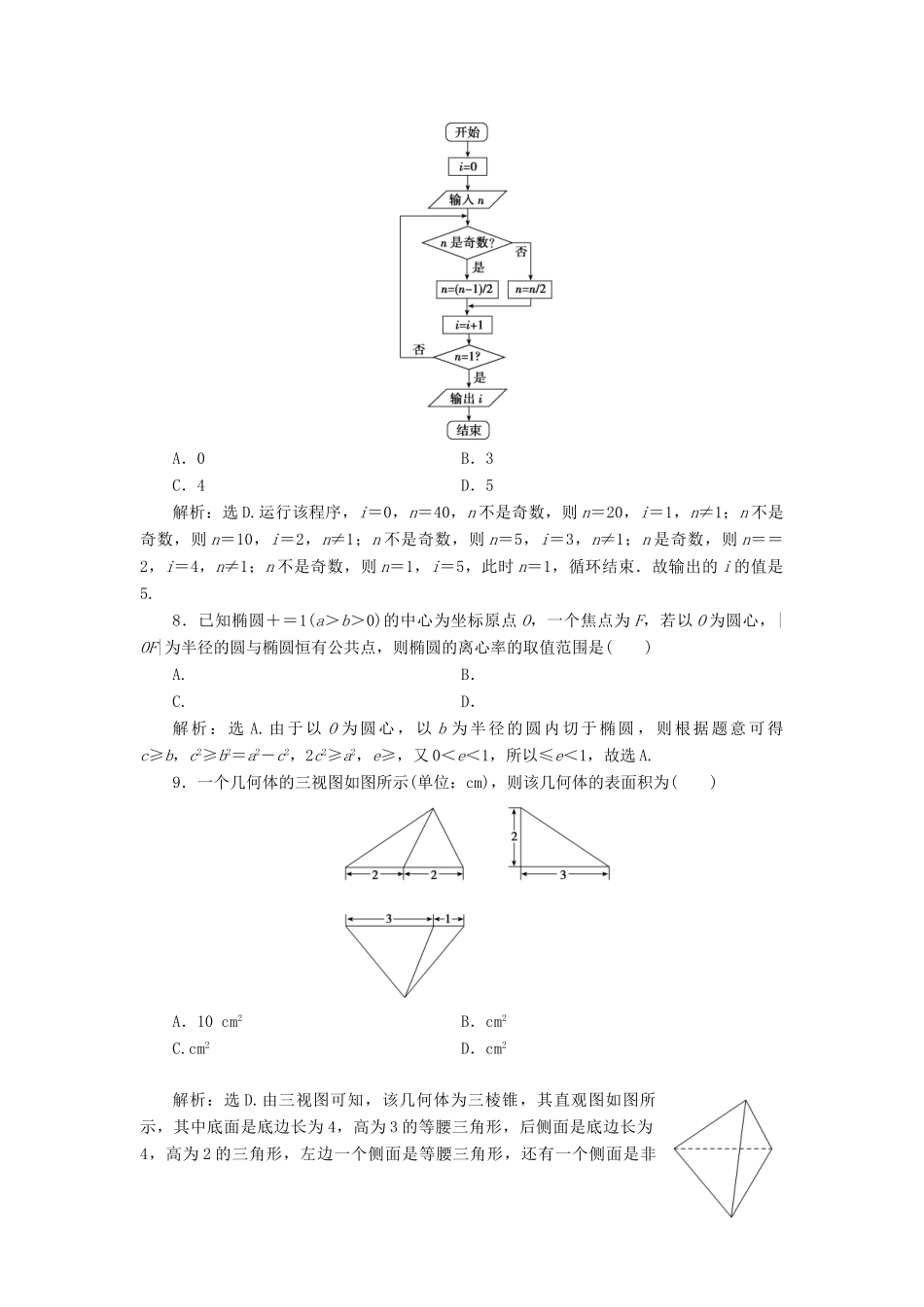
小题提速练(六)一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={x|log2(x-1)<0},B={x|x≥0},则A∩B=()A.(0,1)B.(0,1]C.(1,2)D.(1,2]解析:选C.由log2(x-1)<0可得log2(x-1)<log21,再由函数的定义域和单调性可得0<x-1<1,即1<x<2,从而A=(1,2),A∩B=A=(1,2),选C.2.若复数z满足=3+i(i为虚数单位),则z在复平面内所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限解析:选A.由=3+i,可得z-i=(3+i)(1+i)=2+4i,即z=2+5i,其在复平面内所对应的点(2,5)位于第一象限.3.已知直线l的斜率为k,倾斜角为θ,则“0<θ≤”是“k≤1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解析:选A.当0<θ≤时,0<k≤1;反之,当k≤1时,0≤θ≤或<θ<π,故“0<θ≤”是“k≤1”的充分而不必要条件,选A.4.在区间[0,2]上随机地取一个数x,则事件“2x2-3x≤0”发生的概率为()A.B.C.D.解析:选B.由2x2-3x≤0,得0≤x≤,故所求概率P==,选B.5.cos63°sin177°+sin243°sin87°=()A.B.-C.D.-解析:选D.解法一:cos63°sin177°+sin243°sin87°=cos63°sin(90°+87°)+sin(180°+63°)sin87°=cos63°cos87°-sin63°sin87°=cos(63°+87°)=cos150°=-.解法二:cos63°sin177°+sin243°sin87°=cos63°sin(180°-3°)+sin(180°+63°)sin(90°-3°)=cos63°sin3°-sin63°cos3°=sin(3°-63°)=sin(-60°)=-sin60°=-.6.已知双曲线Γ:-=1(a>b>0)的顶点到渐近线的距离为,且其一个焦点坐标为(5,0),则双曲线Γ的方程为()A.-=1B.-=1C.-=1D.-=1解析:选A.双曲线的一条渐近线方程为bx-ay=0,一个顶点坐标为(a,0),由题有=,而c2=a2+b2且c=5,于是ab=12,联立,得且注意到a>b>0,解得所以双曲线Γ的方程为-=1.7.执行如图所示的程序框图,若输入的n=40,则输出的i的值是()A.0B.3C.4D.5解析:选D.运行该程序,i=0,n=40,n不是奇数,则n=20,i=1,n≠1;n不是奇数,则n=10,i=2,n≠1;n不是奇数,则n=5,i=3,n≠1;n是奇数,则n==2,i=4,n≠1;n不是奇数,则n=1,i=5,此时n=1,循环结束.故输出的i的值是5.8.已知椭圆+=1(a>b>0)的中心为坐标原点O,一个焦点为F,若以O为圆心,|OF|为半径的圆与椭圆恒有公共点,则椭圆的离心率的取值范围是()A.B.C.D.解析:选A.由于以O为圆心,以b为半径的圆内切于椭圆,则根据题意可得c≥b,c2≥b2=a2-c2,2c2≥a2,e≥,又0<e<1,所以≤e<1,故选A.9.一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为()A.10cm2B.cm2C.cm2D.cm2解析:选D.由三视图可知,该几何体为三棱锥,其直观图如图所示,其中底面是底边长为4,高为3的等腰三角形,后侧面是底边长为4,高为2的三角形,左边一个侧面是等腰三角形,还有一个侧面是非特殊三角形,所以表面积S=×4×3+×4×2+××+×××=10+(cm2).10.若函数f(x)=lnx-ax2-4x(a≠0)在区间上单调递增,则实数a的最大值为()A.B.-C.-D.解析:选B.解法一:对函数f(x)求导得f′(x)=-2ax-4=-(x>0).①当a>0时,由f′(x)>0得,0<x<,即f(x)在上单调递增,因为f(x)在区间上单调递增,所以≥,无解,故a不存在;②当-2<a<0时,由f′(x)>0得,0<x<或x>,即f(x)在,上单调递增,因为f(x)在区间上单调递增,所以≥或≤,所以-2<a≤-;③当a≤-2时,f′(x)≥0恒成立,所以f(x)在(0,+∞)上单调递增,符合题意.综上所述,a≤-,即实数a的最大值为-.解法二:对函数f(x)求导得f′(x)=-2ax-4=-(x>0).依题意,得f′(x)≥0在上恒成立,即2ax2+4x-1≤0在上恒成立,所以a≤=在上恒成立,因为∈(3,4),所以a≤-,即实数a的最大值为-.11.某土木工程建筑公司有A,B两种型号的工程车,A,B两种型号的工程车的载重分别为32吨和48吨,该公司承建的工程项目需要将工地的土石从甲地运到乙地.已知A,B两种型号...