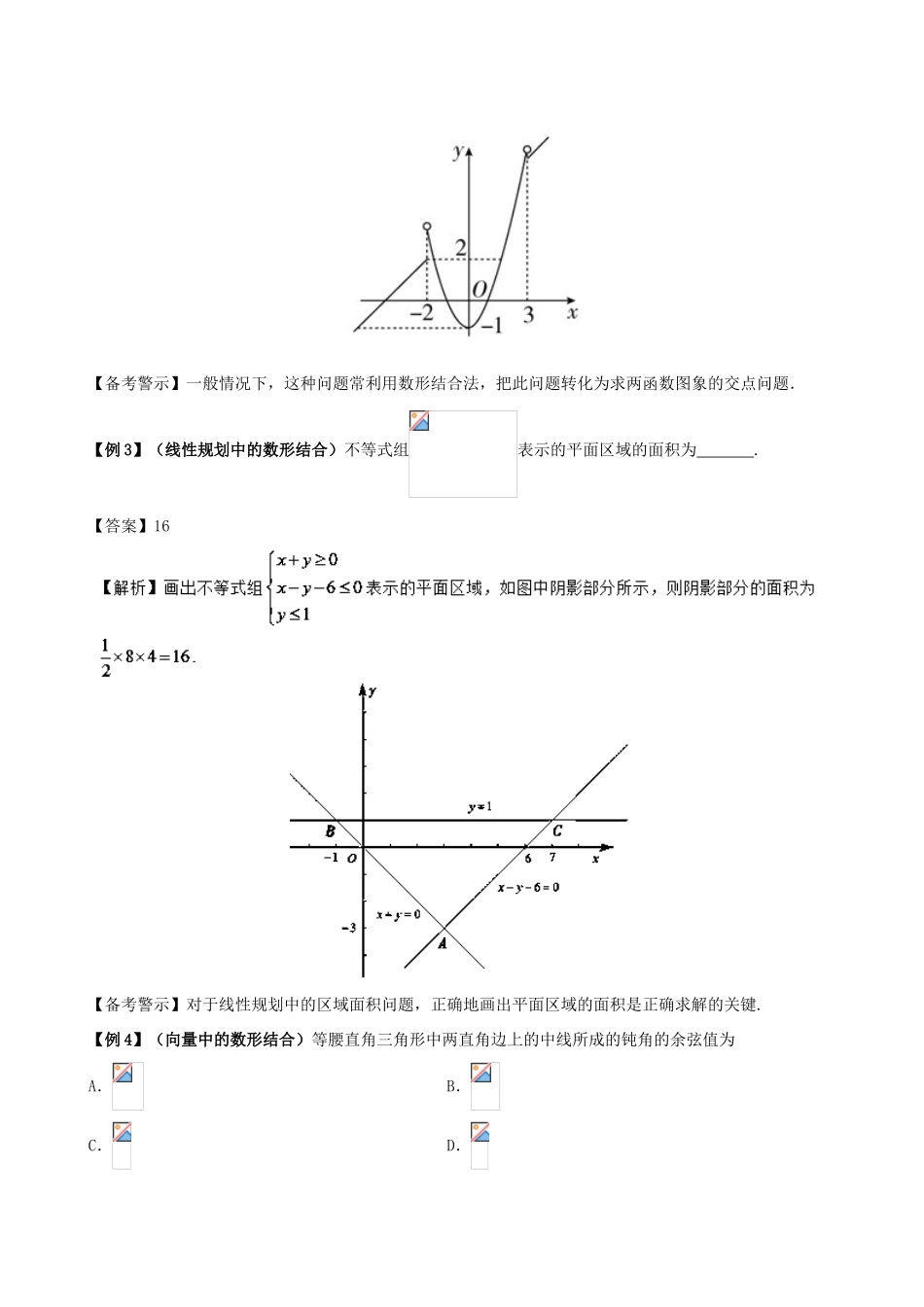
专题05数形结合法方法探究数形结合法,也就是我们常说的图解法,就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的.在高考中,数形结合是一种常用的解题方法,也是一种重要的数学思想方法,特别是在一些计算过程复杂的函数、三角、解析几何等问题中,可以先作出有关函数的图象或者构造适当的几何图形,再利用图示辅助,即参照图形的做法、形状、位置、性质,综合图象的特征进行直观分析,从而得出结论.比如:(1)在集合运算中常常借助于数轴、Venn图来处理集合的交、并、补等运算,从而使问题得以简化,使运算快捷明了.(2)借助于图象研究函数的性质是一种常用的方法.函数图象的几何特征与数量特征紧密结合,体现了数形结合的特征与方法.(3)处理方程问题时,把方程的根的问题看作两个函数图象的交点问题;处理不等式时,从题目的条件与结论出发,联系相关函数,着重分析其几何意义,从图形上找出解题的思路.(4)有关三角函数单调区间的确定或比较三角函数值的大小等问题,一般借助于单位圆或三角函数图象来处理,数形结合思想是处理三角函数问题的重要方法.(5)线性规划问题是在约束条件下求目标函数的最值的问题.从图形上找思路恰好就体现了数形结合思想的应用.(6)数列是一种特殊的函数,数列的通项公式以及前n项和公式可以看作关于正整数n的函数.用数形结合的思想研究数列问题是借助函数的图象进行直观分析,从而把数列的有关问题转化为函数的有关问题来解决.(7)解析几何的基本思想就是数形结合,在解题中善于将数形结合的数学思想运用于对点、线、曲线的性质及其相互关系的研究中.(8)立体几何中用坐标的方法将几何中的点、线、面的性质及其相互关系进行研究,可将抽象的几何问题转化为纯粹的代数运算.著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”数形结合是数学解题中常用的思想方法,数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.所以,我们一定要学好并应用好数形结合的方法.经典示例【例1】(集合中的数形结合)已知集合A=,B=,则AB中元素的个数为A.3B.2C.1D.0【答案】B【名师点睛】求集合的基本运算时,要认清集合元素的属性(是点集、数集或其他情形)和化简集合,这是正确求解集合运算的两个先决条件.集合中元素的三个特性中的互异性对解题影响较大,特别是含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足互异性.【备考警示】对于点集问题,常表示的是某曲线上的点的集合,所以通过画图可以顺利解决此类问题.【例2】(函数中的数形结合)对任意实数a,b定义运算“⊗”:,设,若函数恰有三个零点,则实数k的取值范围是A.(2,1)−B.[0,1]C.[2,0)−D.[2,1)−【答案】D【解析】由新定义可得,即.其图象如图所示,所以由恰有三个零点可得,−1<−k≤2,所以−2≤k<1.故选D.【备考警示】一般情况下,这种问题常利用数形结合法,把此问题转化为求两函数图象的交点问题.【例3】(线性规划中的数形结合)不等式组表示的平面区域的面积为.【答案】16【备考警示】对于线性规划中的区域面积问题,正确地画出平面区域的面积是正确求解的关键.【例4】(向量中的数形结合)等腰直角三角形中两直角边上的中线所成的钝角的余弦值为A.B.C.D.【答案】A【思路点拨】根据已知建立平面直角坐标系,将等腰直角三角形的两直角边所在直线作为x轴和y轴,分别设出三角形顶点和两直角边中点的坐标,再代入坐标求解两中线所对应的向量的数量积和模,进而求得夹角的余弦值.【备考警示】涉及向量的坐标或几何意义时常通过画图进行解决反而更快捷.【例5】(解析几何中的数形结合)已知双曲线C:的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M,N两点.若∠MAN=60°,则C的离心率为_______________.【答案】【解析】如图所示...