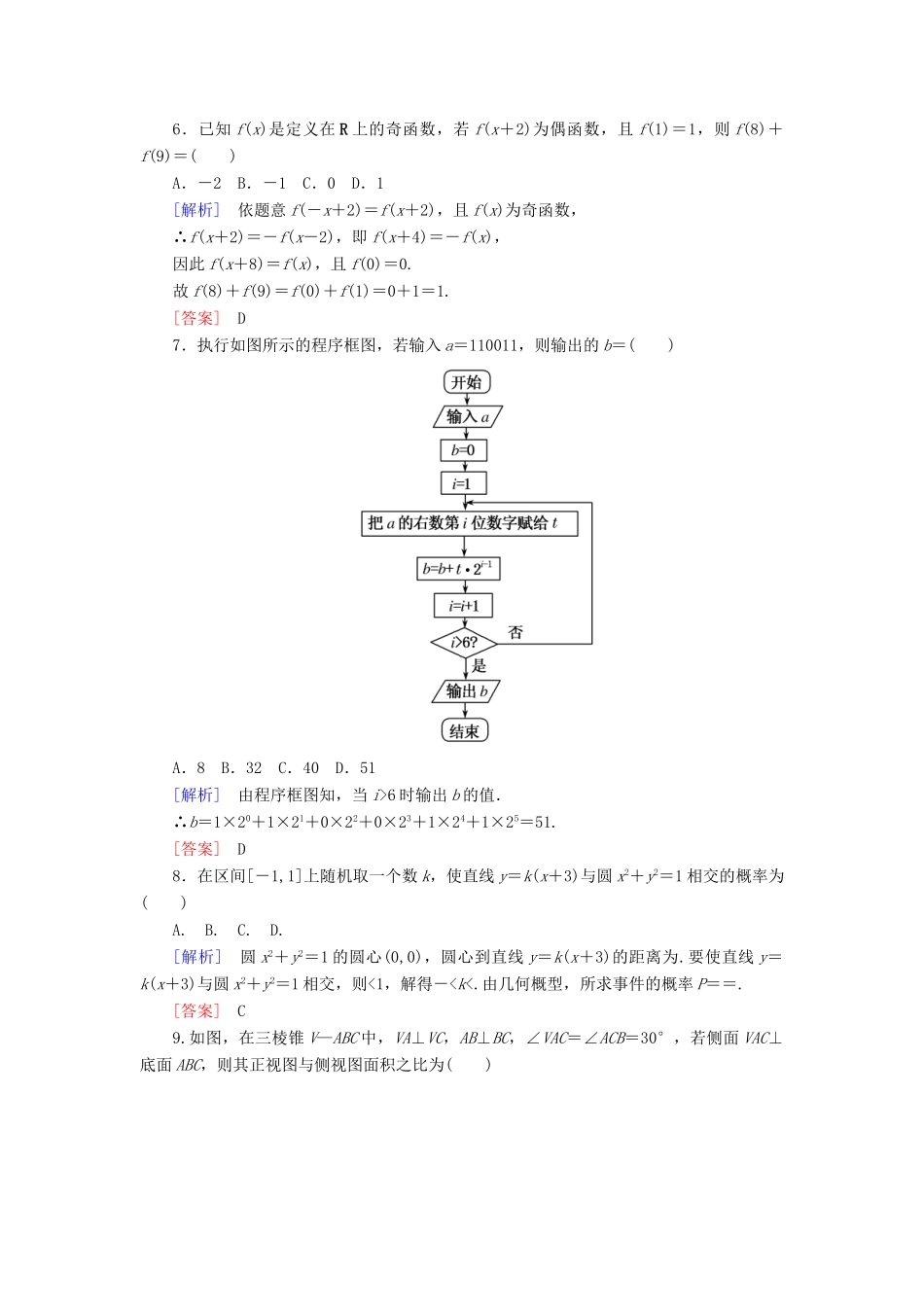
限时标准练(七)(时间:40分钟满分:80分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合A=[-1,2],B={y|y=x2,x∈A},则A∩B=()A.[1,4]B.[1,2]C.[-1,0]D.[0,2][解析] 集合A=[-1,2],B={y|y=x2,x∈A}=[0,4],∴A∩B=[0,2].[答案]D2.欧拉(LeonhardEuler,国籍瑞士)是科学史上最多才的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占有非常重要的地位,被誉为“数学中的天桥”,根据此公式可知,e-4i表示的复数在复平面中位于()A.第一象限B.第二象限C.第三象限D.第四象限[解析]e-4i=cos(-4)+isin(-4), cos(-4)=-cos(4-π)<0,sin(-4)=sin(4-π)>0,∴e-4i表示的复数在复平面中位于第二象限.[答案]B3.已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是()A.p∧qB.p∧綈qC.綈p∧qD.綈p∧綈q[解析]由已知得p真,q假,故綈q真.∴p∧綈q真.[答案]B4.已知平面向量a,b的夹角为,且|a|=1,|b|=,则a+2b与b的夹角是()A.B.C.D.[解析]由题意得a·b=|a||b|cos〈a,b〉=1××cos=.又|a+2b|2=|a|2+4|b|2+4a·b=3,|a+2b|=,(a+2b)·b=a·b+2b2=a·b+2|b|2=,故cos〈a+2b,b〉===,又〈a+2b,b〉∈[0,π].故a+2b与b的夹角是.[答案]A5.在△ABC中,AC=,BC=1,B=60°,则△ABC的面积为()A.B.2C.2D.3[解析] AC=,BC=1,B=60°,∴由余弦定理得AC2=AB2+BC2-2AB·BC·cosB,即13=AB2+1-AB,解得AB=4或-3(舍去),∴S△ABC=AB·BC·sinB=×4×1×=.[答案]A6.已知f(x)是定义在R上的奇函数,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=()A.-2B.-1C.0D.1[解析]依题意f(-x+2)=f(x+2),且f(x)为奇函数,∴f(x+2)=-f(x-2),即f(x+4)=-f(x),因此f(x+8)=f(x),且f(0)=0.故f(8)+f(9)=f(0)+f(1)=0+1=1.[答案]D7.执行如图所示的程序框图,若输入a=110011,则输出的b=()A.8B.32C.40D.51[解析]由程序框图知,当i>6时输出b的值.∴b=1×20+1×21+0×22+0×23+1×24+1×25=51.[答案]D8.在区间[-1,1]上随机取一个数k,使直线y=k(x+3)与圆x2+y2=1相交的概率为()A.B.C.D.[解析]圆x2+y2=1的圆心(0,0),圆心到直线y=k(x+3)的距离为.要使直线y=k(x+3)与圆x2+y2=1相交,则<1,解得-0,|φ|<π)的部分图象如图所示,若将函数f(x)的图象向右平移个单位得到函数g(x)的图象,则函数g(x)的解析式是()A.2sinB.2sinC.2sinD.2cos2x[解析] 由题图象知A=2,T=-=,∴T=π⇒ω=2. 2sin=2,∴可得2×+φ=2kπ+,k∈Z. |φ|<π,∴φ=,则f(x)=2sin.f(x)的图象向右平移个单位后得到的图象解析式为g(x)=2sin=2sin.[答案]A11.已知数列{an}为等差数列,且a1≥1,a2≤5,a5≥8,设数列{an}的前n项和为Sn,S15的最大值为M,最小值为m,则M+m=()A.500B.600C.700D.800[解析]由题意,可知公差最大时,S15最大;公差最小时,S15最小.可得a1=1,a2=5,此时公差d=4是最大值,M=S15=1×15+×4=435.当a2=5,a5=8,此时d=1是最小值,a1=4,m=S15=4×15+×1=165.M+m=435+165=600.[答案]B12.已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲...