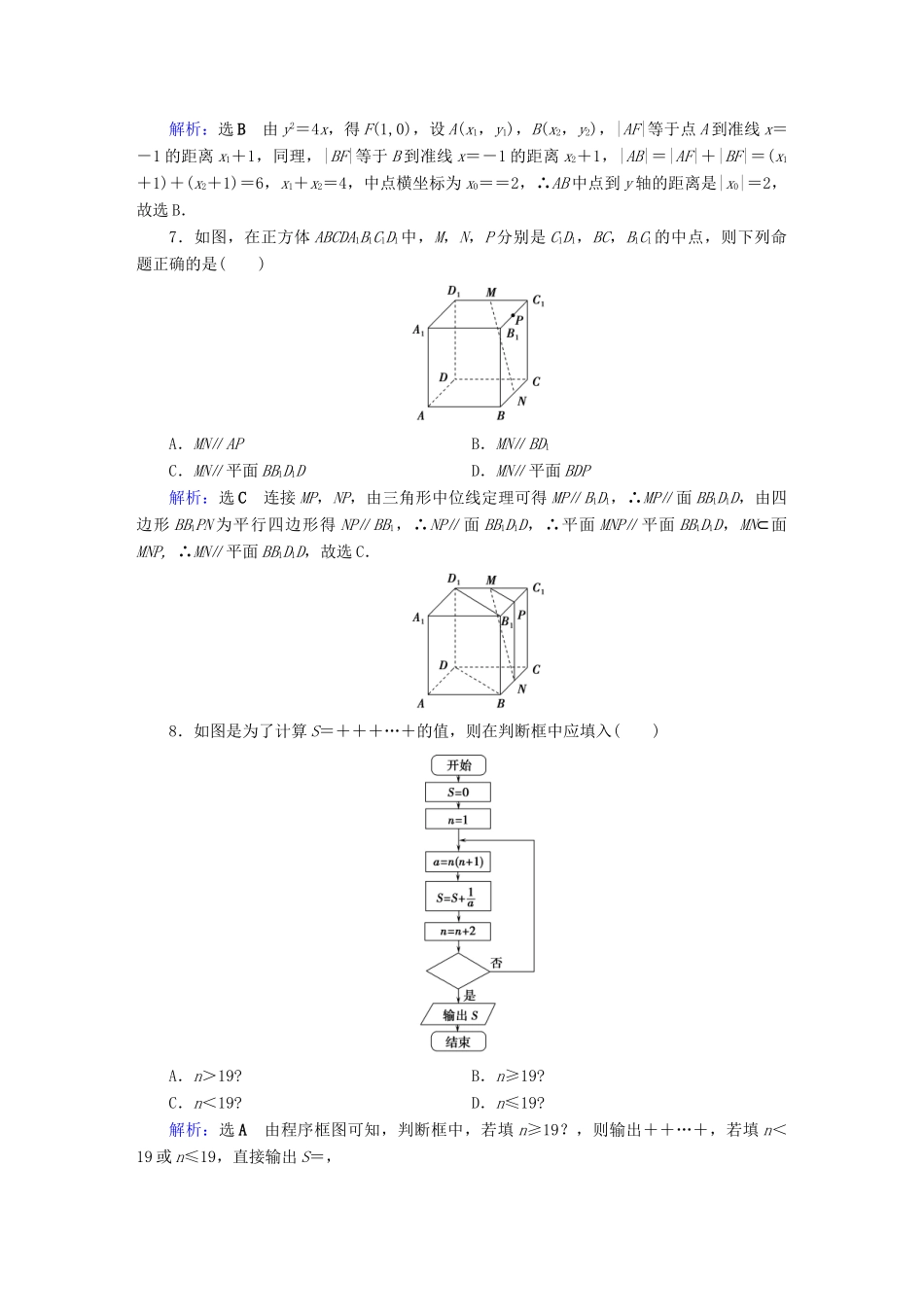
高考小题专练(03)(满分:80分时间:45分钟)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={-1,0,1,2},B={x|x=2n,n∈Z},则A∩B=()A.{2}B.{0,2}C.{-1,0,2}D.∅解析:选B因为集合A={-1,0,1,2},B={x|x=2n,n∈Z},所以A∩B={0,2},故选B.2.复数z满足(2+i)z=|3-4i|,则z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限解析:选D (2+i)z=|3-4i|==5,∴(2-i)(2+i)z=5(2-i),∴z=2-i,z在复平面内对应的点(2,-1),在第四象限,故选D.3.已知f(x)=x3+3x,a=20.3,b=0.32,c=log20.3,则()A.f(a)<f(b)<f(c)B.f(b)<f(c)<f(a)C.f(c)<f(b)<f(a)D.f(b)<f(a)<f(c)解析:选C由指数函数的性质可得,1<a=20.3<21=2,0<b=0.32<0.30=1,由对数函数的性质可得,c=log20.3<log21=0,∴a>b>c,又 f(x)=x3+3x,在R上递增,所以f(c)<f(b)<f(a),故选C.4.如图所示的风车图案中,黑色部分和白色部分分别由全等的等腰直角三角形构成.在图案内随机取一点,则此点取自黑色部分的概率是()A.B.C.D.解析:选B设小黑色三角形面积为S,则整个在图案面积为12S,黑色部分总面积为4S,由几何概型概率公式可得,此点取自黑色部分的概率是=,故选B.5.等差数列{an}的公差为1,a1,a2,a5成等比数列,则{an}的前10项和为()A.50B.-50C.45D.-45解析:选A 等差数列{an}的公差为1,a1,a2,a5成等比数列,∴a=a1a5,即(a1+1)2=a1(a1+4),解得a1=,∴S10=10×+×1=50,故选A.6.已知拋物线C:y2=4x的焦点为F,过F的直线与曲线C交于A,B两点,|AB|=6,则AB中点到y轴的距离是()A.1B.2C.3D.4解析:选B由y2=4x,得F(1,0),设A(x1,y1),B(x2,y2),|AF|等于点A到准线x=-1的距离x1+1,同理,|BF|等于B到准线x=-1的距离x2+1,|AB|=|AF|+|BF|=(x1+1)+(x2+1)=6,x1+x2=4,中点横坐标为x0==2,∴AB中点到y轴的距离是|x0|=2,故选B.7.如图,在正方体ABCDA1B1C1D1中,M,N,P分别是C1D1,BC,B1C1的中点,则下列命题正确的是()A.MN∥APB.MN∥BD1C.MN∥平面BB1D1DD.MN∥平面BDP解析:选C连接MP,NP,由三角形中位线定理可得MP∥B1D1,∴MP∥面BB1D1D,由四边形BB1PN为平行四边形得NP∥BB1,∴NP∥面BB1D1D,∴平面MNP∥平面BB1D1D,MN⊂面MNP,∴MN∥平面BB1D1D,故选C.8.如图是为了计算S=+++…+的值,则在判断框中应填入()A.n>19?B.n≥19?C.n<19?D.n≤19?解析:选A由程序框图可知,判断框中,若填n≥19?,则输出++…+,若填n<19或n≤19,直接输出S=,∴应填n>19?,故选A.9.函数f(x)=sin(ωx+φ)(ω>0)的周期为π,f(π)=,f(x)在上单调递减,则φ的一个可能值为()A.B.C.D.解析:选D由函数f(x)=sin(ωx+φ)(ω>0)的周期为π,得=π,ω=2,f(x)=sin(2x+φ),f(π)=sin(2π+φ)=sinφ=,φ=2kπ+或x=2kπ+π,令k=0,φ=或φ=π,当φ=,2x+∈,f(x)在不是单调函数,∴φ=不合题意,故φ=π,故选D.10.设函数f(x)=若f(x)≥f(1)恒成立,则实数a的取值范围为()A.[1,2]B.[0,2]C.[1,+∞)D.[2,+∞)解析:选A f(x)=若f(x)≥f(1)恒成立,∴f(1)是f(x)的最小值,由二次函数性质可得对称轴a≥1,由分段函数性质得(1-a)2-1≤ln1,得a≤2,综上,1≤a≤2,故选A.11.已知某正三棱锥的侧棱长大于底边长,其外接球体积为,三视图如图所示,则其侧视图的面积为()A.B.2C.4D.6解析:选D设正三棱锥外接球的半径为R,则πR3=⇒R=,由三视图可得底面边长为2,底面正三角形的高为×2=3,底面三角形外接圆半径为×3=2,由勾股定理得2=22+2,得h=4,∴侧视图面积为S△PBE=×3×4=6,故选D.12.设函数f(x)=x-e-x,直线y=mx+n是曲线y=f(x)的切线,则m+n的最小值是()A.-B.1C.1-D.1+解析:选C设切点是P(t,f(t)),由f′(x)=1+e-x,切线斜率k=f′(t)=1+e-t,∴切线方程为y-f(t)=f′(t)(x-t),整理得y=(1+e-t)x-(t+1)e-t...