数学归纳法课件VIP免费

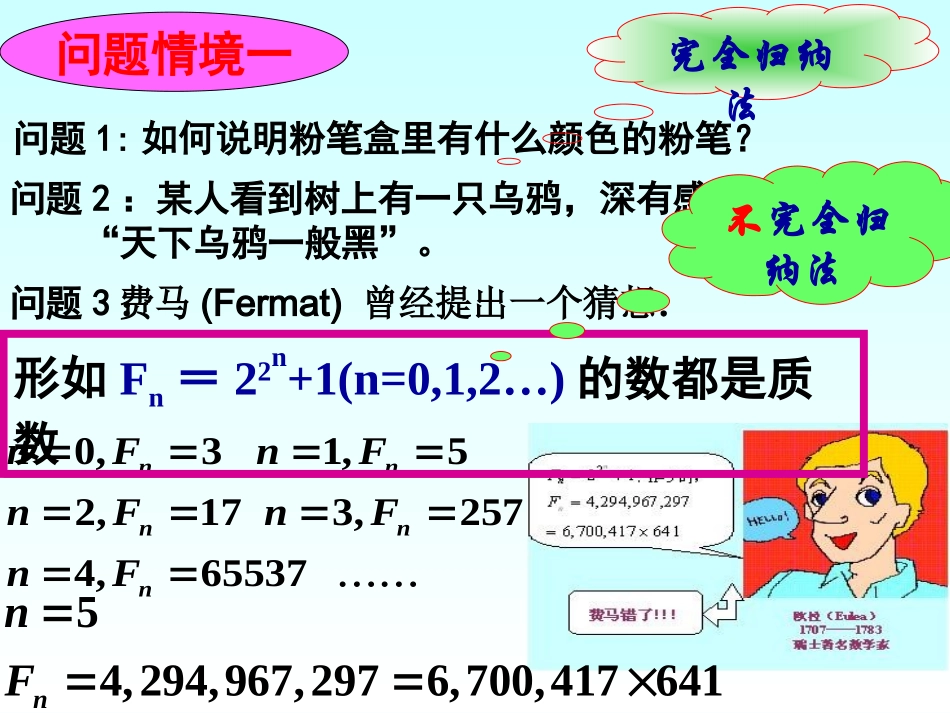
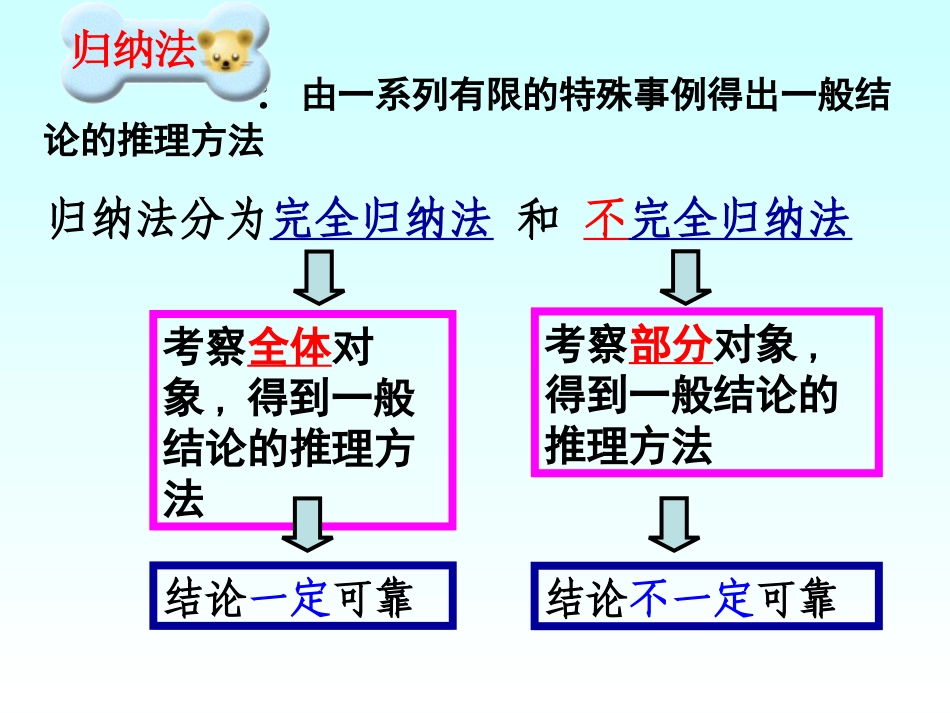
石台中学卢磊问题情境一问题1:如何说明粉笔盒里有什么颜色的粉笔？问题2：某人看到树上有一只乌鸦，深有感触地说：“天下乌鸦一般黑”。54,294,967,2976,700,417641nnF问题3：费马(Fermat)曾经提出一个猜想：0,31,52,173,2574,65537nnnnnnFnFnFnFnF形如Fn＝22n+1(n=0,1,2…)的数都是质数不完全归纳法完全归纳法：由一系列有限的特殊事例得出一般结论的推理方法考察全体对象,得到一般结论的推理方法考察部分对象,得到一般结论的推理方法归纳法分为完全归纳法和不完全归纳法结论一定可靠结论不一定可靠归纳法问题情境二11,11,2,...1nnnnaaaana对于数列已知，猜想其通项公式1nan猜想：如何证明这个猜想的正确性呢？717=a验证:同理得515=a616=a818=a919=a•••正整数无数个!啊,有完没完啊?…212a111a313a414a播放视频你认为证明数列的通项公式是这个猜想与上述多米诺骨牌游戏有相似性吗？你能类比多米诺骨牌游戏解决这个问题吗？（1）当n=1时，猜想成立根据（1）和（2），可知对任意的正整数n，猜想都成立。（1）第一块骨牌倒下。（2）若第k块倒下时，则相邻的第k+1块也倒下。根据（1）和（2），可知不论有多少块骨牌，都能全部倒下。多米诺骨牌游戏原理通项公式为的证明方法1nan（2）若当n=k时猜想成立，即，则当kak1=111+=+kakn=k+1时猜想也成立，即1nan一般地，证明一个与正整数n有关的数学命题，可按下列步骤进行：（1）证明当n取第一个值n0(例如n0=1)时命题成立;（2）假设当n=k(k∈N*,k≥n0)时命题成立证明当n=k+1时命题也成立。由(1)(2)可知命题对从开始的所有正整数n都成立。这种证明方法叫做数学归纳法数学归纳法【归纳递推】【归纳奠基】0n1）第一步应做什么？此时n0=，左=，2）假设n=k时命题成立，即6)12)(1(3212222kkkk当n=k时，等式左边共有项，第k项是。kk2思考？6)12)(1(3212222nnnn112例1用数学归纳法证明Nn3）当n=k+1时，命题的形式是61)1(21)1()1()1(32122222kkkkk4）此时，左边增加的项是2)1(k5)从左到右如何变形？6)12)(1(3212222nnnn例1用数学归纳法证明Nn222222)1(6)12)(1()1(321kkkkkk6)1(6)12)(1(2kkkk6)672)(1(2kkk6)32)(2)(1(kkk61)1(21)1()1(kkk证明：6)12)(1(3212222kkkk那么当n=k+1时，（2）假设当n=k时，等式成立，即（1）当n=1时左边＝12＝1，右边＝1，等式成立。222222)1(6)12)(1()1(321kkkkkk6)672)(1(2kkk6)32)(2)(1(kkk61)1(21)1()1(kkk这就是说，当n=k+1时等式也成立根据（1）和（2），可知等式对任何nN∈＊都成立如上证明是否存在问题，为什么？第二步证明中没有用到假设，这不是数学归纳法证明。课堂练习：用数学归纳法证明:当Nn2)12(..........531nn证明：①当n=1时，左边＝1,右边=1②设n=k时，有2)12(.........531kk2)1k(2)1k](1)1k(21[]1)1k(2[)1k2(...........531即n=k+1时，命题成立。根据①②可知，对nN∈＊，等式成立。等式成立。那么，当n=k+1时，证明:(1)当n=1时左＝1，右＝12＝1∴n=1时，等式成立(2)假设n=k时，等式成立，即1+3+5+…+(2k1)=k2那么，当n=k+1时左＝1+3+5+…+(2k1)＋[2(k+1)-1]=k2+2k+1=(k+1)2=右即n=k+1时命题成立由(1)、(2)可知等式对任何nN*都成立递推基础递推依据正解：一，数学归纳法是一种证明与正整数有关的数学命题的重要方法。主要有两个步骤、一个结论:（1）证明当n取第一个值n0（如n0=1或2等）时命题成立（2）假设n=k时命题正确，证明n=k+1时命题也成立（3）由（1）、（2）得出结论归纳小结二，数学归纳法也是一种完全归纳法，它是在可靠的基础上，利用命题自身具有的传递性，运用“有限”的手段，来解决“无限”的问题，它克服了完全归纳法的繁杂，不可行的特点，又克服了不完全归纳法结论不可靠的不足，使我们认识到事情由简到繁，由特殊到一般，由有限到无限的过程。作业:P96A组1，2课堂练习2：P95练习1、2；