数学二模参考答案与评分标准VIP免费

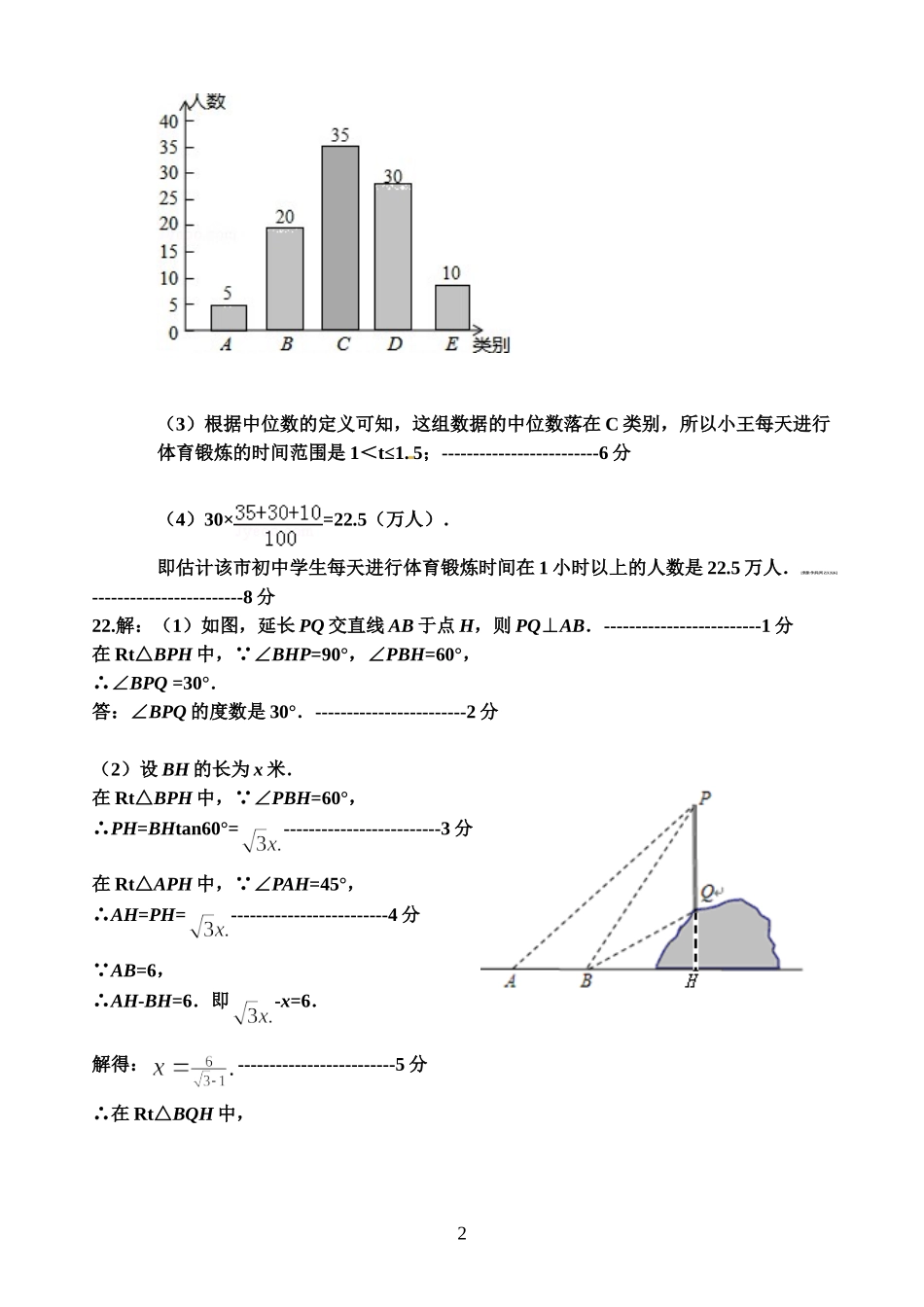
12016初中毕业学业考试模拟考试（二）参考答案及评分标准一、选择题（本大题共10小题，每小题3分，满分30分）1---10题：ABCDACBCAB二、填空题（本大题共8小题，每小题3分，满分24分）11.5.12.13.71°.14.8-2π．15.2.16.2∶3．17.＜m＜218.①③⑤三、解答题（本大题共2小题，每小题6分，满分12分）19.解：原式=2+3﹣2﹣3﹣1-----------------4分=﹣1．-----------------6分20.解：原式=xxxxxxxxx1])1()1()1)(1()1(2[2=xxxxxx1)112(=xxxx11=11xx，-----------------3分（1）当3x时，原式=1313=2；-----------------4分（2）要使原式的值为-1，也就是111xx，则)1(1xx，0x，-----------------5分但是当0x时，原式无意义，所以原代数式的值不能等于-1。-----------------6分四、解答题（本大题共2小题，每小题8分，满分16分）21.解：（1）a=100﹣（5+20+30+10）=35．故答案为35；-------------------------2分（2）补全条形统计图如下所示：-------------------------4分2（3）根据中位数的定义可知，这组数据的中位数落在C类别，所以小王每天进行体育锻炼的时间范围是1＜t≤1.5；-------------------------6分（4）30×=22.5（万人）．即估计该市初中学生每天进行体育锻炼时间在1小时以上的人数是22.5万人．[来源:学|科|网Z|X|X|K]------------------------8分22.解：（1）如图，延长PQ交直线AB于点H，则PQ⊥AB．-------------------------1分在Rt△BPH中， ∠BHP=90°，∠PBH=60°，∴∠BPQ=30°．答：∠BPQ的度数是30°．------------------------2分（2）设BH的长为x米．在Rt△BPH中， ∠PBH=60°，∴PH=BHtan60°=-------------------------3分在Rt△APH中， ∠PAH=45°，∴AH=PH=-------------------------4分 AB=6，∴AH-BH=6．即-x=6．解得：-------------------------5分∴在Rt△BQH中，3-------------------------6分在△BPQ中， ∠BPQ=∠PBQ=30°，∴PQ=BQ=．-------------------------7分答：该电线杆PQ的高度约为()米．-------------------------8分五、解答题（本大题共2小题，每小题9分，满分18分）23.解：（1）设一支钢笔需x元，一本笔记本需y元--------------------------1分由题意得：2x+3y=625x+y=90-------------------------3分解得x=16y=10-------------------------5分答：一支钢笔需16元，一本笔记本需10元-------------------------6分（2）设购买m支钢笔，则购买笔记本（80-m）本.由题意得：16m+10（80-m）≤1100-------------------------7分解得m≤50-------------------------8分答：最多可以购买50支钢笔.-------------------------9分24.解：（1）证明： AC=CE=CB=CD，∠ACB=∠ECD=90°，∴∠A=∠B=∠D=∠E=45°．-----------------1分在△BCF和△ECH中，，∴△BCF≌△ECH（ASA），-----------------4分∴CF=CH（全等三角形的对应边相等）；-----------------5分（2）解：四边形ACDM是菱形．-----------------6分证明： ∠ACB=∠DCE=90°，∠BCE=45°，∴∠1=∠2=45°． ∠E=45°，∴∠1=∠E，∴AC∥DE，-----------------7分∴∠AMH=180°﹣∠A=135°=∠ACD，又 ∠A=∠D=45°，∴四边形ACDM是平行四边形（两组对角相等的四边形是平行四边形），----------------8分4 AC=CD，∴四边形ACDM是菱形．-----------------9分六、解答题（本大题共2小题，每小题10分，满分20分）25.解：（1）证明： ∠EAD=EBC∠，∠BCE=ADE∠，∴△AEDBEC∽△，-----------------2分∴，EA•EC=EB•ED∴；-----------------3分（2）证明：如图2，连接CD，OB交AC于点FB 是弧AC的中点，BAC=ADB=ACB∴∠∠∠，且AF=CF=0.5AC．-----------------4分又 AD为⊙O直径，ABC=90°∴∠，又∠CFB=90°．CBFABD∴△∽△．-----------------5分∴，故CF•AD=BD•BC．AC•AD=2BD•CD∴；-----------------6分（3）解：如图3，连接AO并延长交⊙O于F，连接DF，AF∴为⊙O的直径，ADF=90°∴∠，-----------------7分过O作OHAD⊥于H，AH=DH∴，OHDF∥，-----------------8分AO=OF ，DF=2OH=4∴，ACBD ⊥，AEB=ADF=...