新课标2010届高三物理二轮复习专题课件：学案6《万有引力定律的应用》VIP免费

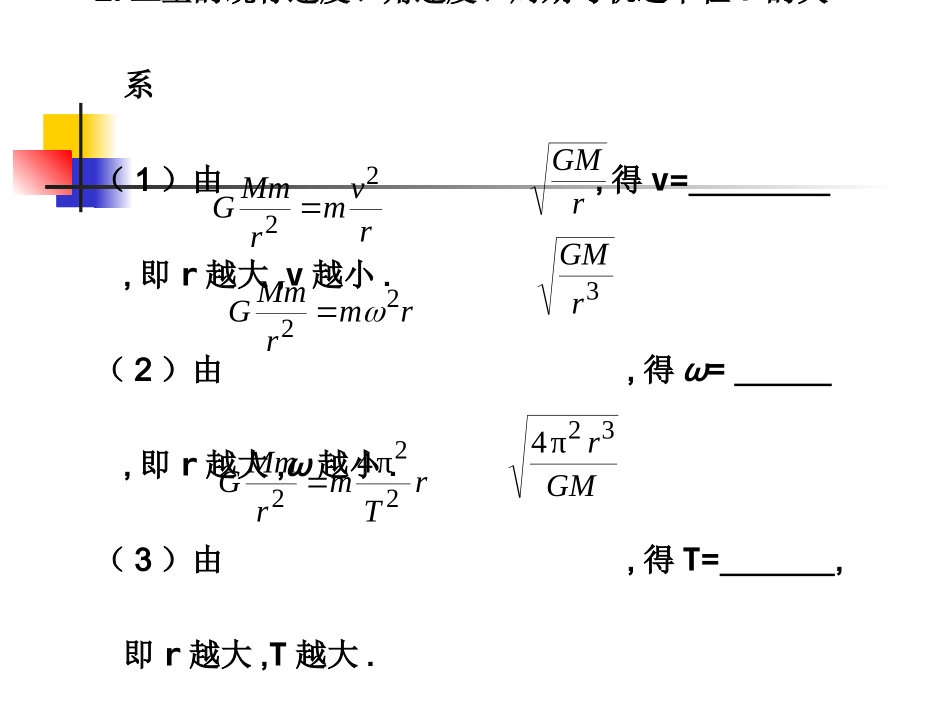
学案万有引力定律的应用知识回顾1.在处理天体的运动问题时,通常把天体的运动看成是运动,其所需要的向心力由提供.其基本关系式为:.在天体表面,忽略自转的情况下有:.匀速圆周万有引力rfmrTmrmrvmrMmG22222)π2()π2(mgRMmG22.卫星的绕行速度、角速度、周期与轨道半径r的关系（1）由,得v=,即r越大,v越小.（2）由,得ω=,即r越大,ω越小.（3）由,得T=,即r越大,T越大.rvmrMmG22rGM3rGMGMr32π4rmrMmG22rTmrMmG222π43.三种宇宙速度（1）第一宇宙速度（环绕速度）:v1=,是人造地球卫星的最小发射速度.（2）第二宇宙速度（脱离速度）:v2=,使物体挣脱地球引力束缚的最小发射速度.（3）第三宇宙速度（逃逸速度）:v3=,使物体挣脱太阳引力束缚的最小发射速度.7.9km/s11.2km/s16.7km/s4.天体质量M、密度ρ的估算测出卫星绕天体做匀速圆周运动的半径r和周期T,由r0为天体的半径.当卫星沿天体表面绕天体运行时,r=r0,则ρ=.30232222π34,π4π4rMVMGTrMrTmrMmG得3023π3rGTr2π3GT方法点拨1.分析天体运动类问题的一条主线就是F万=F向,抓住黄金代换GM=.2.近地卫星的线速度即第一宇宙速度,是卫星绕地球做圆周运动的最大速度,也是发射卫星的最小速度.3.因卫星上物体的重力用来提供绕地球做圆周运动的向心力,所以均处于状态,与重力有关的仪器不能使用,与重力有关的实验不能进行.4.卫星变轨时,离心运动后速度变,向心运动后速度变.5.确定天体表面重力加速度的方法有:①测重力法;②单摆法;③（或竖直上抛）物体法;④近地卫星环绕法.gR2完全失重小大平抛类型一万有引力定律及其应用例1（2009·南京模拟）图1所示是我国的“探月工程”向月球发射一颗绕月探测卫星“嫦娥一号”的过程简图.“嫦娥一号”进入月球轨道后,在距离月球表面高为h的轨道上绕月球做匀速圆周运动.图1（1）若已知月球半径为R月,月球表面的重力加速度为g月,则“嫦娥一号”环绕月球运行的周期为多少?（2）若已知R月=R地,g月=g地,则近月卫星的运行速度约为近地卫星运行速度的多少倍？4161解析（1）设“嫦娥一号”环绕月球运行的周期是T,根据牛顿第二定律得月月mgRMmG2)(π4)(222hRTmhRΜmG月月解得T=（2）对于靠近天体表面的行星或卫星有mg=,v=由v=知,将R月=R地,g月=g地代入计算,可知222)(π4月月月RghRRmv2gR地地月月地月RgRgvvgR4161126地月vv答案（1）（2）解题归纳万有引力提供天体或卫星做匀速圆周运动的向心力是解决这类问题最基本的一个关系.222)(π4月月月RghR126预测1“嫦娥一号”探月卫星发动机关闭，轨道控制结束，卫星进入地月转移轨道.图2中MN之间的一段曲线表示转移轨道的一部分，P是轨道上的一点，直线AB过P点且和两边轨道相切.下列说法中正确的是（）A.卫星在此段轨道上，动能一直减小B.卫星经过P点时动能最小C.卫星经过P点时速度方向由P向BD.卫星经过P点时加速度为零BCD图2类型二中心天体质量、密度的计算例2把地球绕太阳公转看作匀速率圆周运动，轨道平均半径约为1.5×108km,已知万有引力常量G=6.67×10-11N·m2/kg2,则可估算出太阳的质量大约是多少?（结果取一位有效数字）解析题干给出地球轨道半径r=1.5×108km,虽没直接给出地球运转周期数值，但日常知识告诉我们：地球绕太阳公转一周为365天，故周期T=365×24×3600s=3.2×107s.万有引力提供向心力,故太阳质量rTmrMmG22)π2(M=≈2×1030kg.27113112222)102.3(1067.6)105.1(14.34π4GTr答案2×1030kg解题归纳求天体的质量、密度通过观察天体做匀速率圆周运动的卫星的周期T、半径r,由万有引力等于向心力,得天体质量M=.（1）若知天体的半径R，则天体的密度ρ=.rTmrMmG222π4222π4GTr3232π3π34RGTrRMVM（2）若天体的卫星环绕天体表面运动，其轨道半径r等于天体半径R，其周期为T，则天体密度ρ=.2π3GT预测2美国“勇气”号火星车在火星表面成功登陆，登陆时间选择在6万年来火星距地球最近的一次，火星与地球之间的距离仅有5580万千米，火星车在登陆前绕火星做圆周运动，距火星表面高度为H，火星半径为R，绕行N圈的时间为t.求：（1）若地球、火星绕太阳公转为匀速圆周运动，其周期分别为T地、T火，...