选修2-3_231离散型随机变量的均值和方差VIP免费

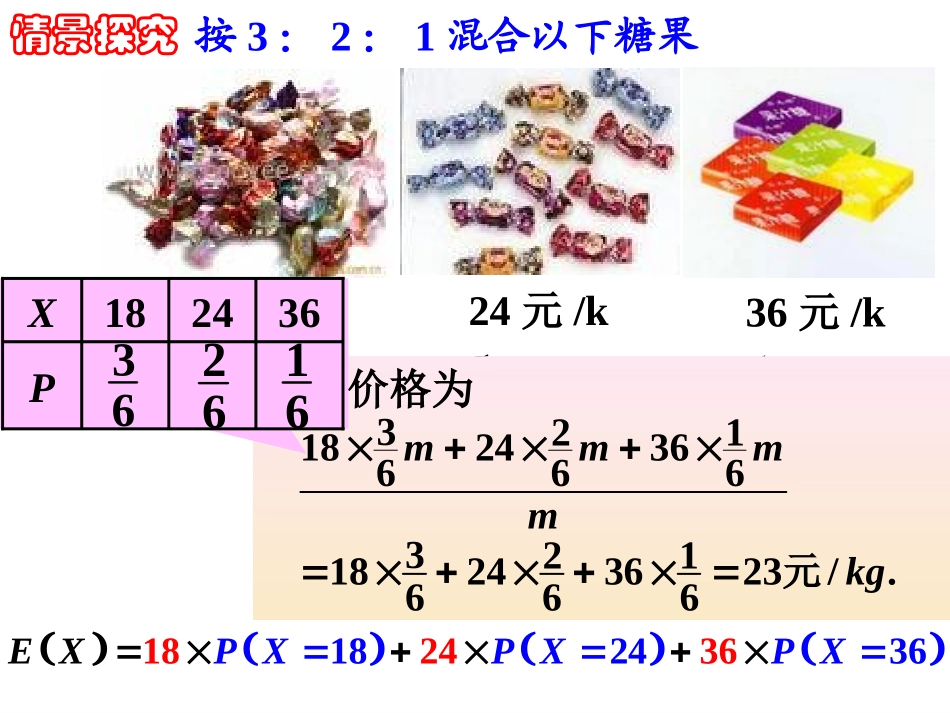
2.3.1离散型随机变量的均值按3：2：1的比例混合，混合糖果中每一粒糖果的质量都相等.定价为混合糖果的平均价格才合理问题情景18元/kg24元/kg36元/kgm千克混合糖果的总价格为321182436666mmm18元/kg24元/kg36元/kg情景探究按3：2：1混合以下糖果182436182436PXPXPEXX平均价格为32118243666632118243623/.666mmmmkg元362418PX362616均值(数学期望)定义一般地，若离散型随机变量X的概率分布为XP1x2x3xnx1p2p3pnp1122nnXEXxpxpxp均值则称为随机变量的或，它反映了离散型随机变量取值的平数学期望均水平.随机变量均值的线性性质已知随机变量X，其均值为E(X).若Y＝aX＋b，其中a，b为常数，则Y也是随机变量．并且随机变量Y的均值为：E(Y)=E(aX＋b)＝aE(X)＋b．P654321X161616161616P13119753Y161616161616例如随机抛掷一个骰子，求所得骰子的点数X的均值.定义随机变量Y=2X+1，求E(Y).1122112212()()()...()(...)(...)().nnnnnEYaxbpaxbpaxbpaxpxpxpbpppaEXbpnxn……pkxk……p2x2p1x1PXpnaxn+b……pkaxk+b……p2ax2+bp1ax1+bPX随机变量X的分布列为：随机变量Y=aX+b的分布列为：随机变量Y的数学期望是：在篮球比赛中，罚球命中1次得1分，不中得0分.如果某运动员罚球命中的概率为0.7，那么他罚球1次的得分X的均值是多少？X=1或X=0P(X=1)=0.7X10P0.70.3()10.700.30.7.EX那么他罚球100次的得分X的均值是多少？温故知新一般地，如果随机变量X服从两点分布，那么E(X)=？()10(1).EXppp若X服从两点分布，则E(X)=p.X01P1－pp深入探究深入探究如果X~B(n，p)，那么E(X)=？1110.nkknknknpCpqnp若X~B(n，p)，则E(X)=np.111(1)101()nnkknkkknknnkkEXkCpqnpCpq()1(012)nkkknPXkCppkn，，，…，11.kknnkCnC这里用到，请自己证明则E(X)＝p若X~H(N，M，n)则E(X)＝nMN若X~B(n，p)则E(X)＝np若X~B(1，p)各种不同概率模型下的数学期望例1甲、乙两名射手射击的环数为两个相互独立的随机变量X与Y，且X，Y的分布列为：问：甲、乙两名射手谁的射击水平高?X123P0.30.10.6Y123P0.30.40.3()10.320.130.62.3EX；()10.320.430.32.0.EY所以，甲射手比乙射手的射击水平高.解：例题讲解设在一组数据x1，x2，…，xn中，各数据与它们的平均数的差的平方的平均值是：叫做这组数据的方差.2222121()()()nSxxxxxxn方差说明了这组数据的波动情况.离散型随机变量的方差定义对于离散型随机变量X的概率分布如下表：(其中pi≥0，i＝1，2，…，n；p1＋p2＋…＋pn＝1)Xx1x2…xnPp1p2…pn(xi－E(X))2描述了xi(i=1，2，…，n)相对于均值E(X)的偏离程度，故(x1－E(X))2p1＋(x2－E(X))2p2＋...＋(xn－E(X))2pn称为离散型随机变量X的方差，记为D(X).其算术平方根为X的标准差：记为()DX().X随机变量的方差与标准差都反映了随机变量取值的稳定与波动，集中与分散的程度.离散型随机变量的方差定义定义深析随机变量的方差和样本的方差有何联系和区别？012P0.40.20.4012P0.10.80.1甲工人：乙工人：例1甲、乙两名工人加工同一种零件，两人每天加工的零件相等，所得次品数分别是、，分布列如下：、解：1122()9()0.4()9()0.8.EDED，；，从上可知，.所以，在射击之前，可以预测甲、乙两名射手所得环数的平均值很接近，均在9环左右，但射手甲所得的环数比较集中，得9环较多，而射手乙所得环数比较分散，得8环和10环的次数要多些.1212()()()()EEDD，例题讲解例2甲、乙两名射手在同一条件下进行射击，分布列如下表：射手甲射手乙用击中环数的期望与方差分析比较两名射手的射击水平.0.4100.290.48概率p击中环数0.2100.690.28概率p击中环数(3)~1()(1)XBpDXpp若，，则；2(2)()()DaXbaDX；212221122()(())(())(())(())niiinnDXxEXpxEXpxEXpxEXp...