课后提升作业二十七指数型、对数型函数模型的应用举例(45分钟70分)一、选择题(每小题5分,共40分)1.(2016·兰州高一检测)光线通过一块玻璃,其强度要失掉原来的,要使通过玻璃的光线强度为原来的以下,至少需要重叠这样的玻璃块数是(lg3=0.4771)()A.10B.11C.12D.13【解析】选B.设原光线的强度为a,重叠x块玻璃后,通过玻璃的光线强度为y,则y=a(x∈N*),令y
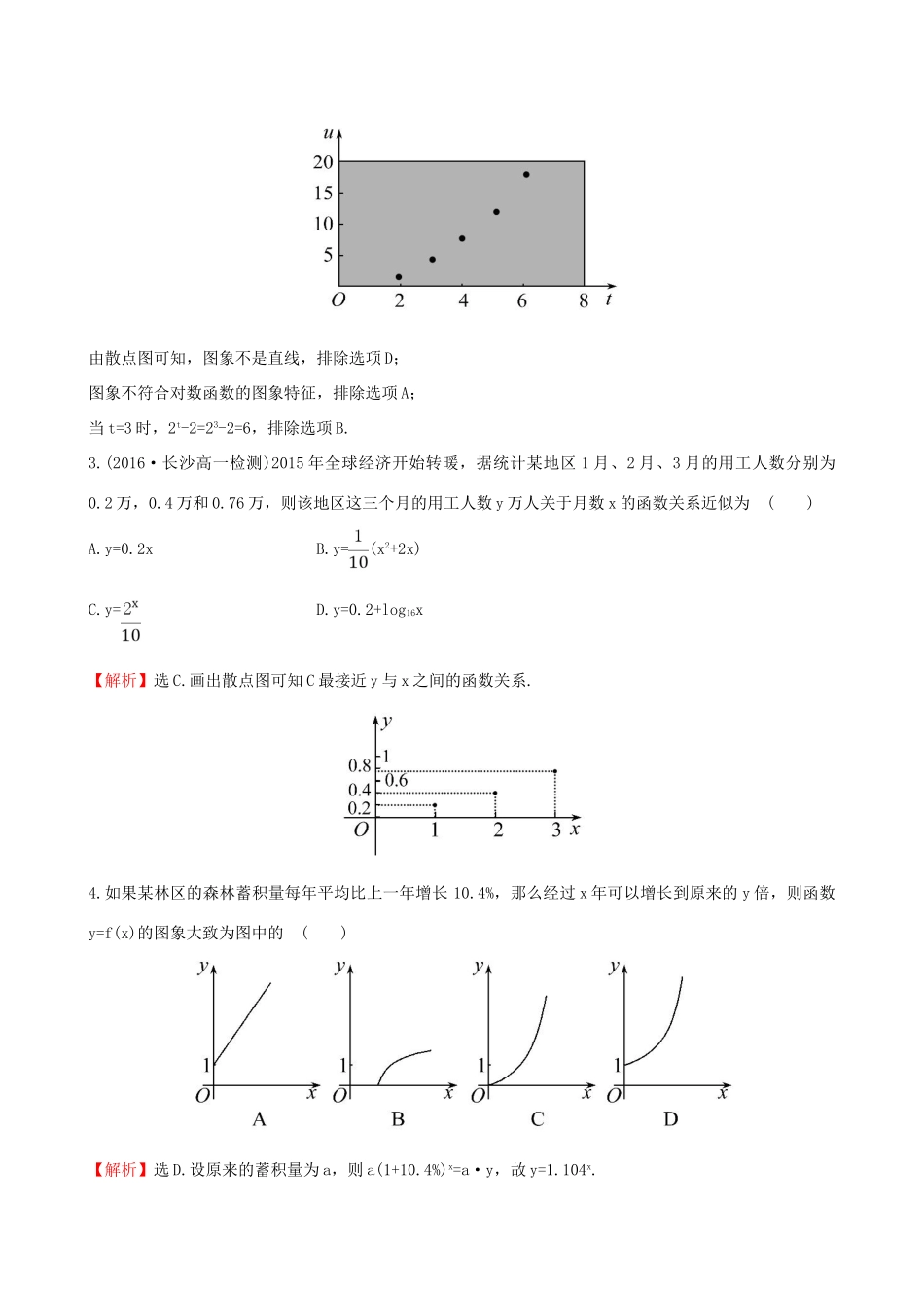
.因为==≈10.4,即x>10.4.所以x最小为11,即至少需要重叠11块这样的玻璃.2.今有一组实验数据如下表所示:t1.993.04.05.16.12u1.54.047.51218.01则能体现这些数据关系的函数模型是()A.u=log2tB.u=2t-2C.u=D.u=2t-2【解析】选C.可以先画出散点图,并利用散点图直观地认识变量间的关系,选择合适的函数模型来刻画它.散点图如图所示.由散点图可知,图象不是直线,排除选项D;图象不符合对数函数的图象特征,排除选项A;当t=3时,2t-2=23-2=6,排除选项B.3.(2016·长沙高一检测)2015年全球经济开始转暖,据统计某地区1月、2月、3月的用工人数分别为0.2万,0.4万和0.76万,则该地区这三个月的用工人数y万人关于月数x的函数关系近似为()A.y=0.2xB.y=(x2+2x)C.y=D.y=0.2+log16x【解析】选C.画出散点图可知C最接近y与x之间的函数关系.4.如果某林区的森林蓄积量每年平均比上一年增长10.4%,那么经过x年可以增长到原来的y倍,则函数y=f(x)的图象大致为图中的()【解析】选D.设原来的蓄积量为a,则a(1+10.4%)x=a·y,故y=1.104x.【延伸探究】本题中的条件“经过x年可以增长到原来的y倍”若换为“经过y年可以增长到原来的x倍”.其他条件不变,结论又如何呢?【解析】选B.设原来的蓄积量为a,则a(1+10.4%)y=a·x,即y=log1.104x,故选B.5.已知函数t=-144lg的图象可表示打字任务的“学习曲线”,其中t(h)表示达到打字水平N(字/min)所需的学习时间,N表示打字速度(字/min),则按此曲线要达到90字/min的水平,所需的学习时间是()A.144hB.90hC.60hD.40h【解析】选A.由N=90可知,t=-144lg=144h.6.今有一组数据,如表所示:x12345y356.999.0111下列函数模型中,最接近地表示这组数据满足的规律的一个是()A.指数函数B.反比例函数C.一次函数D.二次函数【解析】选C.画出散点图,如图所示.观察散点图,可见各个点接近于一条直线,所以可用一次函数表示.【补偿训练】某研究小组在一项实验中获得一组数据,将其整理得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是()A.y=2tB.y=2t2C.y=t3D.y=log2t【解题指南】观察散点图结合已学函数图象可得结果.【解析】选D.根据散点图可知与对数函数一致.7.某种细菌在培养的过程中,每15分钟分裂一次(由一个分裂成两个),则这种细菌由一个分裂成4096个需经过()A.12小时B.4小时C.3小时D.2小时【解析】选C.设需经过x次分裂,则4096=2x,解得x=12,所以时间t==3小时.8.向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是()【解析】选B.图反映随着水深h的增加,注水量V增长速度越来越慢,这反映水瓶中水上升的液面越来越小.二、填空题(每小题5分,共10分)9.如图,开始时桶1中有a升水,如果桶1向桶2注水,桶1中剩余的水符合指数衰减曲线y1=a·e-nt(n为常数,t为注水时间),那么桶2中的水就是y2=a-a·e-nt.如果由桶1向桶2中注水5分钟时,两桶中的水相等,那么经过分钟桶1中的水只有.【解析】由于t=5时两桶中的水相等,所以a·e-n×5=a-a·e-n×5,所以(e-n)5=,即e-n=.由条件可得a·e-nt=,即=,所以t=15.答案:1510.在不考虑空气阻力的情况下,火箭的最大速度v米/秒和燃料的质量M千克、火箭(除燃料外)的质量m千克的函数关系式是v=2000·ln.当燃料质量是火箭质量的倍时,火箭的最大速度可达12千米/秒.【解题指南】燃料质量与火箭质量的倍数即为的值,只需将v=12000代入原式中求的值即可.【解析】当v=12000时,2000·ln=12000,所以ln=6,所以=e6-1.答案:e6-1三、解答题(每小题10分,共20分)11.(2016·晋江高一检测)某同学在这次学校运动会时不慎受伤,校医给他开了一些消炎药,要求他每天定时服一片.现知该药片含药量为200mg,他的肾脏...