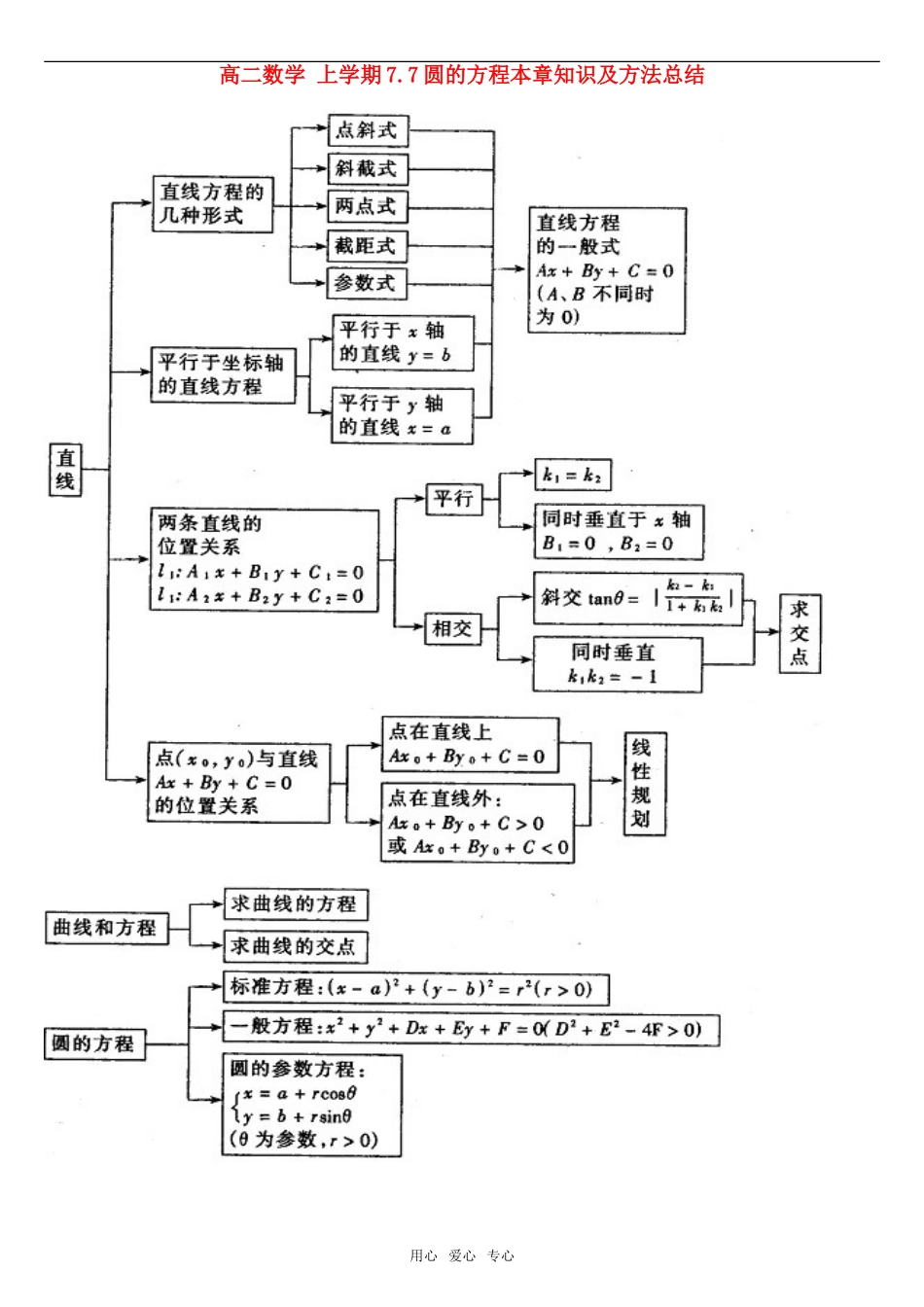
高二数学上学期7.7圆的方程本章知识及方法总结用心爱心专心2.知识纲要(1)直线的倾斜角和斜率的概念,过两点的直线的斜率公式,由一点和斜率导出直线方程的方法;直线方程的点斜式、两点式、参数式和直线方程的一般式,根据条件求直线的方程.(2)两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式;根据直线的方程判断两条直线的位置关系.(3)二元一次不等式表示平面区域.简单的线性规划问题,线性规划的意义及应用.(4)坐标法研究几何问题、圆的标准方程、圆的一般方程、圆的参数方程.●方法总结1.建立直角坐标系,通过研究曲线的方程研究曲线是解析几何的基本思想,它揭示了数学中“数”与“形”的内在联系.2.曲线(含直线)的交点问题转化为两曲线的方程组成的方程组的解的问题,体现了方程的思想.3.简单的线性规划问题转化为平行直线系在某个区域上截距的最值问题.4.两个条件决定一条直线,三个条件决定一个圆.在确定直线和圆的方程时,常用到待定系数法.[例1]直线(a<b<)的倾斜角是A.B.C.D.选题意图:考查直线的倾斜角和斜率的概念.解析:∵直线的斜率,设直线的倾斜角为,则.∴.答案:A说明:本题涉及了直线的斜率、直线的倾斜角以及反三角函数的有关知识,是一道小综合题.用反三角函数表示直线的倾斜角时,要注意反三角函数的值域以及倾斜角的范围.[例2]已知点A(0,2)和圆C:,一条光线从A点出发射到x轴上后沿圆的切线方向反射,求这条光线从A点到切点所经过的路程.选题意图:考查圆及圆的切线的性质.解:设反射光线与圆相切于D点.点A关于x轴的对称点的坐标为A1(0,-2),则光从A点到切点所走的路程为|A1D|.在Rt△A1CD中,∴|A1D|=.即光线从A点到切点所经过的路程是.说明:此例的解法关键是利用A关于x轴的对称点A1在反射光线上,把光线从A点到折射点再到切点D的路程,转化为求线段A1D的长.本例的其他解法都不如这个解法简便.用心爱心专心