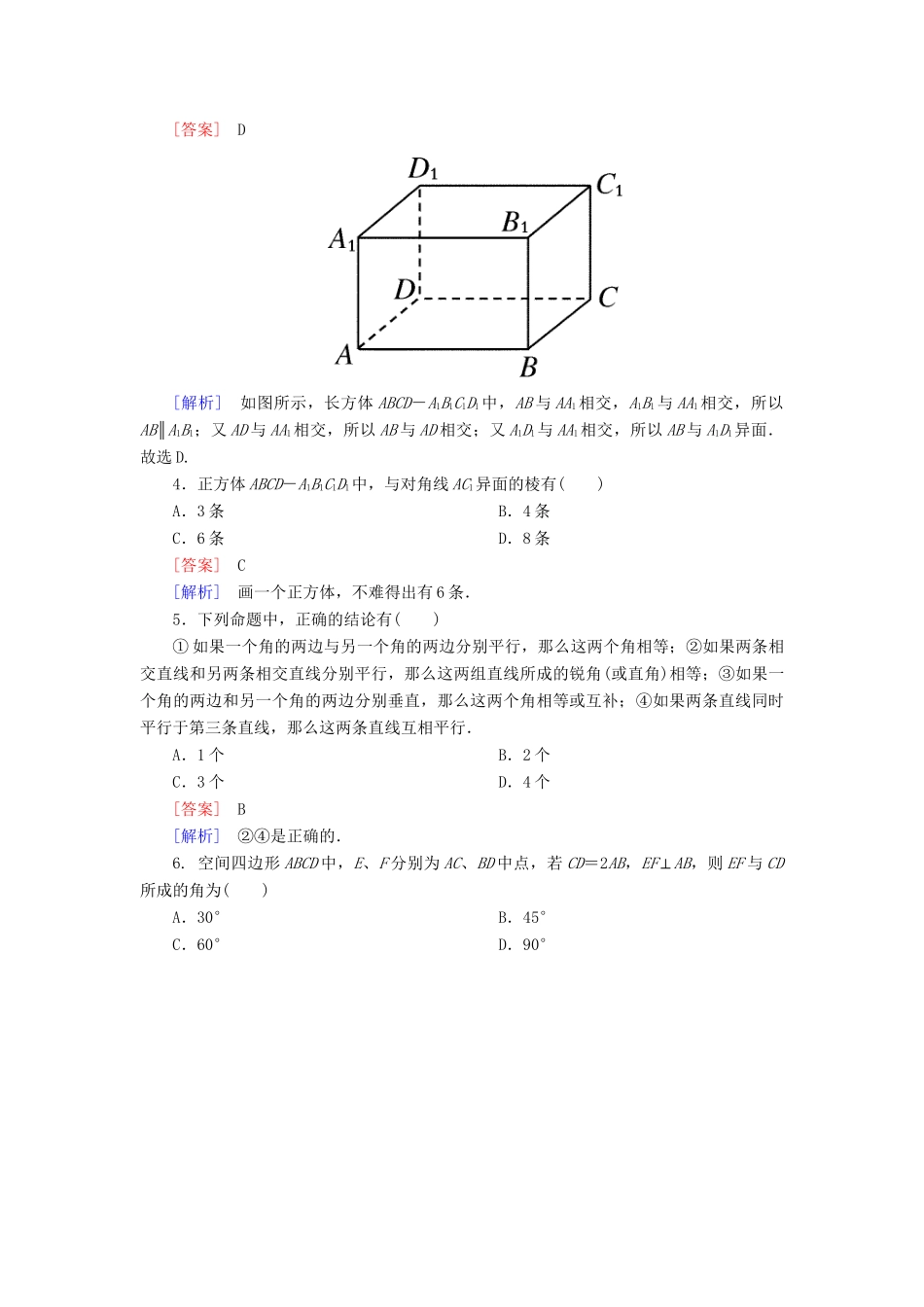
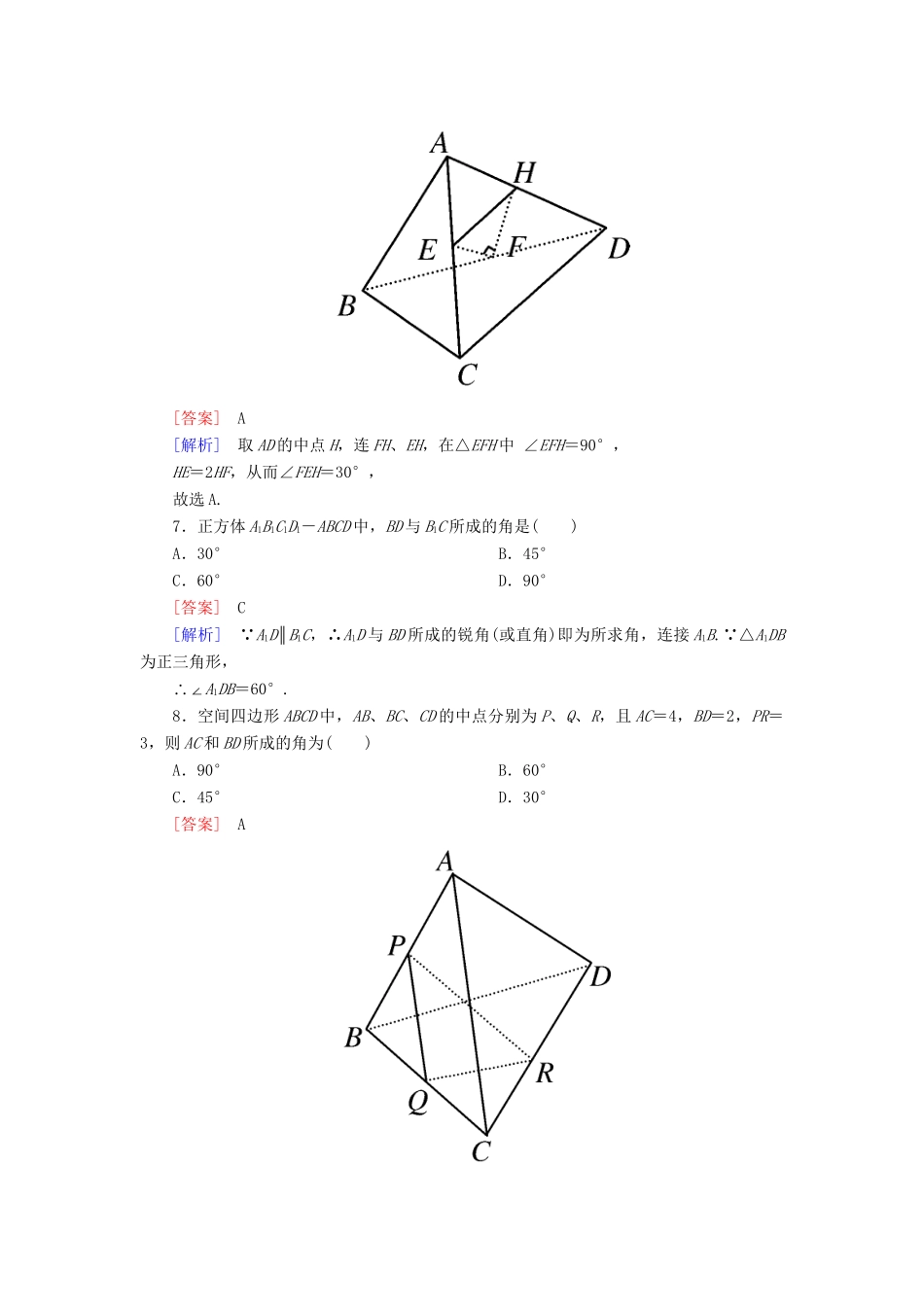
【成才之路】高中数学2-1-2空间中直线与直线之间的位置关系能力强化提升新人教A版必修2一、选择题1.异面直线是指()A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线[答案]D[解析]对于A,空间两条不相交的直线有两种可能,一是平行(共面),另一个是异面.∴A应排除.对于B,分别位于两个平面内的直线,既可能平行也可能相交也可异面,如右图,就是相交的情况,∴B应排除.对于C,如右图的a,b可看做是平面α内的一条直线a与平面α外的一条直线b,显然它们是相交直线,∴C应排除.只有D符合定义.∴应选D.规律总结:解答这类立体几何的命题的真假判定问题,一方面要熟练掌握立体几何中的有关概念和公理、定理;另一方面要善于寻找特例,构造相关特例模型,能快速、有效地排除相关的选择项.2.a,b为异面直线,且a⊂α,b⊂β,若α∩β=l,则直线l必定()A.与a,b都相交B.与a,b都不相交C.至少与a,b之一相交D.至多与a,b之一相交[答案]C[解析]若a,b与l都不相交,则a∥l,b∥l,即a∥b,与a,b是异面直线矛盾.故选C.3.直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是()A.相交B.平行C.异面D.以上都有可能[答案]D[解析]如图所示,长方体ABCD-A1B1C1D1中,AB与AA1相交,A1B1与AA1相交,所以AB∥A1B1;又AD与AA1相交,所以AB与AD相交;又A1D1与AA1相交,所以AB与A1D1异面.故选D.4.正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有()A.3条B.4条C.6条D.8条[答案]C[解析]画一个正方体,不难得出有6条.5.下列命题中,正确的结论有()①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;②如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等;③如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补;④如果两条直线同时平行于第三条直线,那么这两条直线互相平行.A.1个B.2个C.3个D.4个[答案]B[解析]②④是正确的.6.空间四边形ABCD中,E、F分别为AC、BD中点,若CD=2AB,EF⊥AB,则EF与CD所成的角为()A.30°B.45°C.60°D.90°[答案]A[解析]取AD的中点H,连FH、EH,在△EFH中∠EFH=90°,HE=2HF,从而∠FEH=30°,故选A.7.正方体A1B1C1D1-ABCD中,BD与B1C所成的角是()A.30°B.45°C.60°D.90°[答案]C[解析] A1D∥B1C,∴A1D与BD所成的锐角(或直角)即为所求角,连接A1B. △A1DB为正三角形,∴∠A1DB=60°.8.空间四边形ABCD中,AB、BC、CD的中点分别为P、Q、R,且AC=4,BD=2,PR=3,则AC和BD所成的角为()A.90°B.60°C.45°D.30°[答案]A[解析]如图,P、Q、R分别为AB、BC、CD中点,∴PQ∥AC,QR∥BD,∴∠PQR为AC和BD所成角又PQ=AC=2,QR=BD=,RP=3∴PR2=PQ2+QR2,∴∠PQR=90°即AC和BD所成的角为90°,故选A.二、填空题9.分别在两个平面内的两条直线的位置关系是________,不平行的两条直线的位置关系是________,两条直线没有公共点,则它们的位置关系是________,垂直于同一直线的两条直线的位置关系为________.[答案]平行、相交、异面相交、异面平行、异面平行、相交、异面.10.若AB∥A′B′,AC∥A′C′,则下列结论:①∠ACB=∠A′C′B′;∠ABC+∠A′B′C′=180°;∠BAC=∠B′A′C′或∠BAC+∠B′A′C′=180°.一定成立的是________.[答案]③11.正方体ABCD-A1B1C1D1的棱长为a、M、N、P、Q分别为棱AB、BC、C1D1和CC1的中点,则①MN与PQ的位置关系为________,它们所成的角为________.②DB1与MN的位置关系为________,它们所成的角是________.[答案]①相交60°②异面90°[解析]①连接AC、D1C由于P、Q分别为C1D1、C1C的中点,所以PQ∥D1C,同理MN∥AC,则AC与D1C所成角即为MN与PQ所成角,∠D1CA=60°.②连接AC、BD交于O,取BB1的中点H,连OH,则OH∥B1D,连AH,HC,则AH=HC,∴OH⊥AC,又MN∥AC,OH∥B1D,∴MN⊥B1D.12.正方体ABCD-A1B1C1D1中①AC和DD1所成角是________度.②AC和D1C1所成的角是________度.③AC和B1D1所成的角是_____...