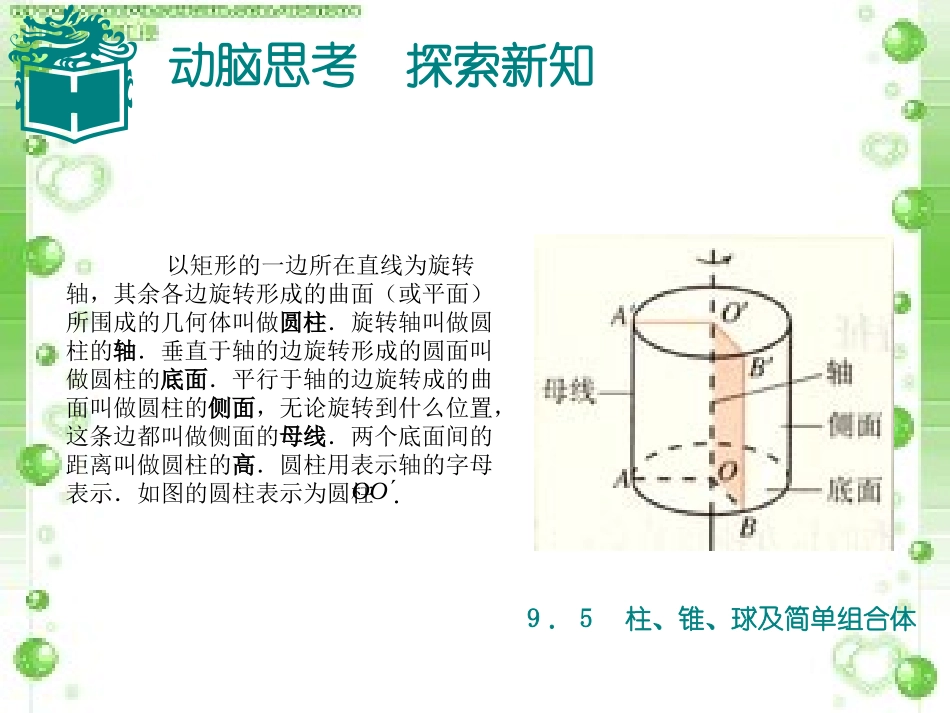
第九章立体几何9.5柱、锥、球及简单组合体创设情境兴趣导入9.5柱、锥、球及简单组合体以矩形的一边所在直线为旋转轴旋转,观察其余各边旋转一周所形成的几何体动脑思考探索新知9.5柱、锥、球及简单组合体以矩形的一边所在直线为旋转轴,其余各边旋转形成的曲面(或平面)所围成的几何体叫做圆柱.旋转轴叫做圆柱的轴.垂直于轴的边旋转形成的圆面叫做圆柱的底面.平行于轴的边旋转成的曲面叫做圆柱的侧面,无论旋转到什么位置,这条边都叫做侧面的母线.两个底面间的距离叫做圆柱的高.圆柱用表示轴的字母表示.如图的圆柱表示为圆柱OO.9.5柱、锥、球及简单组合体动脑思考探索新知观察圆柱(图9−64),可以得到圆柱的下列性质(证明略):(1)圆柱的两个底面是半径相等的圆,且互相平行;(2)圆柱的母线平行且相等,并且等于圆柱的高;(3)平行于底面的截面是与底面半径相等的圆;(4)轴截面是宽为底面的直径、长为圆柱的高的矩形9.5柱、锥、球及简单组合体动脑思考探索新知圆柱的侧面积、全面积(表面积)、及体积的计算公式如下:2Srh圆柱侧p2()Srhr圆柱全p2Vrh圆柱p其中r为底面半径,h为圆柱的高.9.5柱、锥、球及简单组合体巩固知识典型例题例3已知圆柱的底面半径为1cm,体积为5πcm3,求圆柱的高与全面积.解由于底面半径为1cm,所以π5πh解得圆柱的高为5h(cm).所以圆锥的全面积为22()12cmSrhr圆柱全pp创设情境兴趣导入9.5柱、锥、球及简单组合体以直角三角形的一条直角边为旋转轴进行旋转,观察旋转一周所形成的几何体9.5柱、锥、球及简单组合体动脑思考探索新知以直角三角形的一条直角边为旋转轴旋转一周,其余各边旋转而形成的曲面(或平面)所围成的几何体叫做圆锥(如图).旋转轴叫做圆锥的轴.另一条直角边旋转而成的圆面叫做底面.斜边旋转而成的曲面叫做侧面,无论旋转到什么位置,斜边都叫做侧面的母线.母线与轴的交点叫做顶点.顶点到底面的距离叫做圆锥的高.圆锥用表示轴的字母表示.如图所示的圆锥表示为圆锥SO.9.5柱、锥、球及简单组合体动脑思考探索新知观察圆锥,可以得到圆锥的下列性质(证明略):(1)平行于底面的截面是圆;(2)顶点与底面圆周上任意一点的距离都相等,且等于母线的长度;(3)轴截面为等腰三角形,其底边上的高等于圆锥的高.圆锥的侧面积、全面积(表面积)及体积的计算公式如下:Srl圆锥侧p()Srlr圆锥全p213Vrh圆锥p其中r为底面半径,l为母线长,h圆锥的高.巩固知识典型例题9.5柱、锥、球及简单组合体例4已知圆锥的母线的长为2cm,圆锥的高为1cm,求该圆锥的体积.解由图知223cmrlh故圆锥的体积为231(3)1cm3V圆锥创设情境兴趣导入9.5柱、锥、球及简单组合体半圆以其直径所在的直线为旋转轴进行旋转,观察旋转一周所形成的几何体动脑思考探索新知9.5柱、锥、球及简单组合体以半圆的直径所在的直线为旋转轴旋转一周,所形成的曲面叫做球面(如图).球面围成的几何体叫做球体,简称球.半圆的圆心叫做球心,半圆的半径叫做球的半径.经常用表示球心的字母来表示球,如图中所示的球记作球O.ABCOR动脑思考探索新知9.5柱、锥、球及简单组合体如图所示,用平面去截球,观察截面的图形.由实验可以得到球的如下性质(证明略):球的截面是圆面,并且球心与截面圆心的连线垂直于截面.设球心到截面的距离为d,球的半径为R,截面上圆的半径为r(如图),则22rRd经过球心的平面截球面所得的圆叫做球的大圆.此时d=0,r=R,截得的圆半径最大.不经过球心的平面截球面所得的圆叫做球的小圆.动脑思考探索新知9.5柱、锥、球及简单组合体把地球近似地看作一个球时,经线就是球面上从北极到南极的半个大圆;赤道是一个大圆,其余的纬线都是小圆.如左图所示.经过球面上两点的大圆在这两点间的一段劣弧(指不超过半个大圆的弧)AB的长度就是A、B两点的球面距离.飞的长度叫做两点的球面距离.它是球面上这两点之间最短连线的长度,右图的劣弧机、轮船都是尽可能以大圆弧为两点间的航线航行的.动脑思考探索新知9.5柱、锥、球及简单组合体球的表面积与体积的计算公式如下:2...