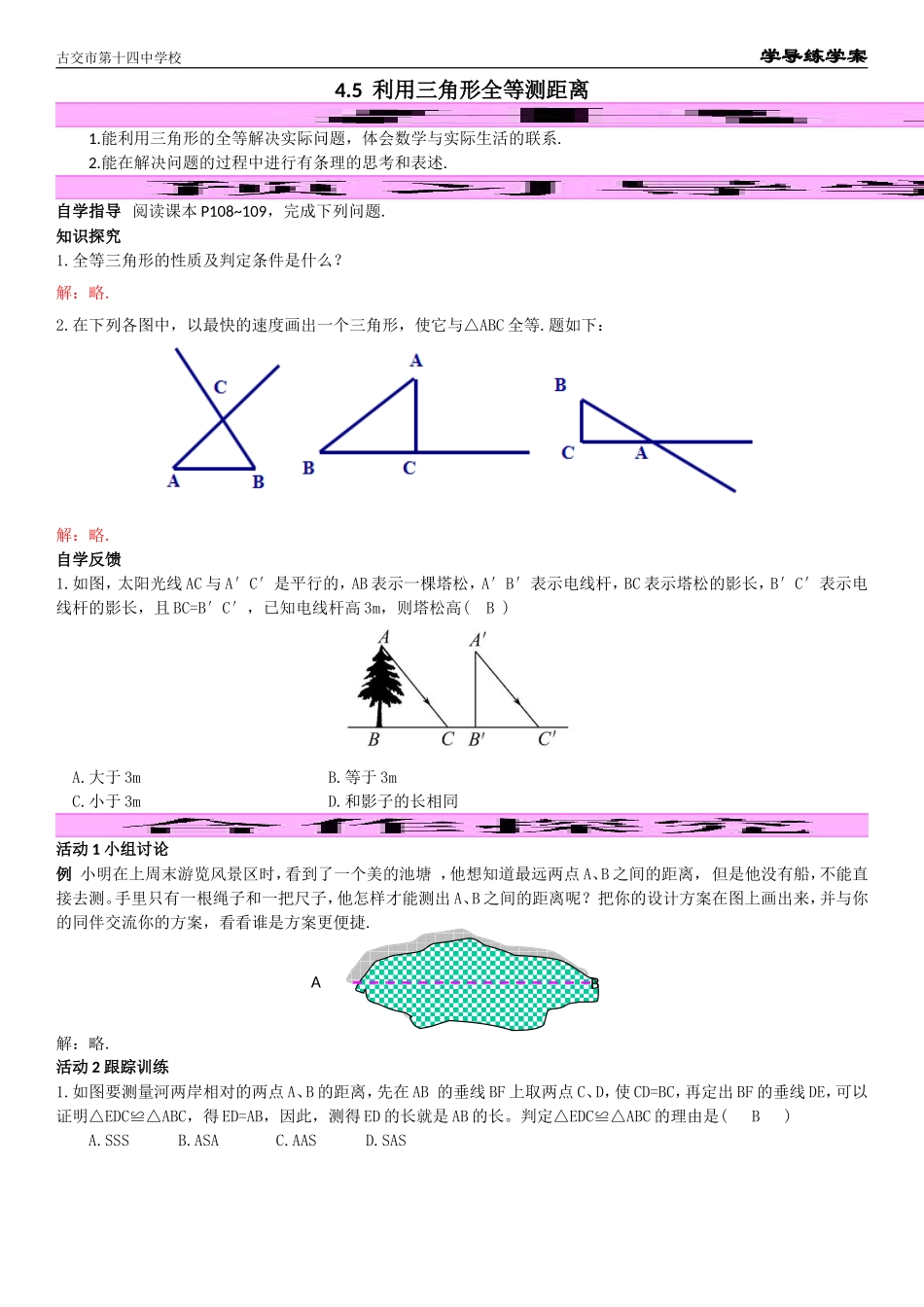
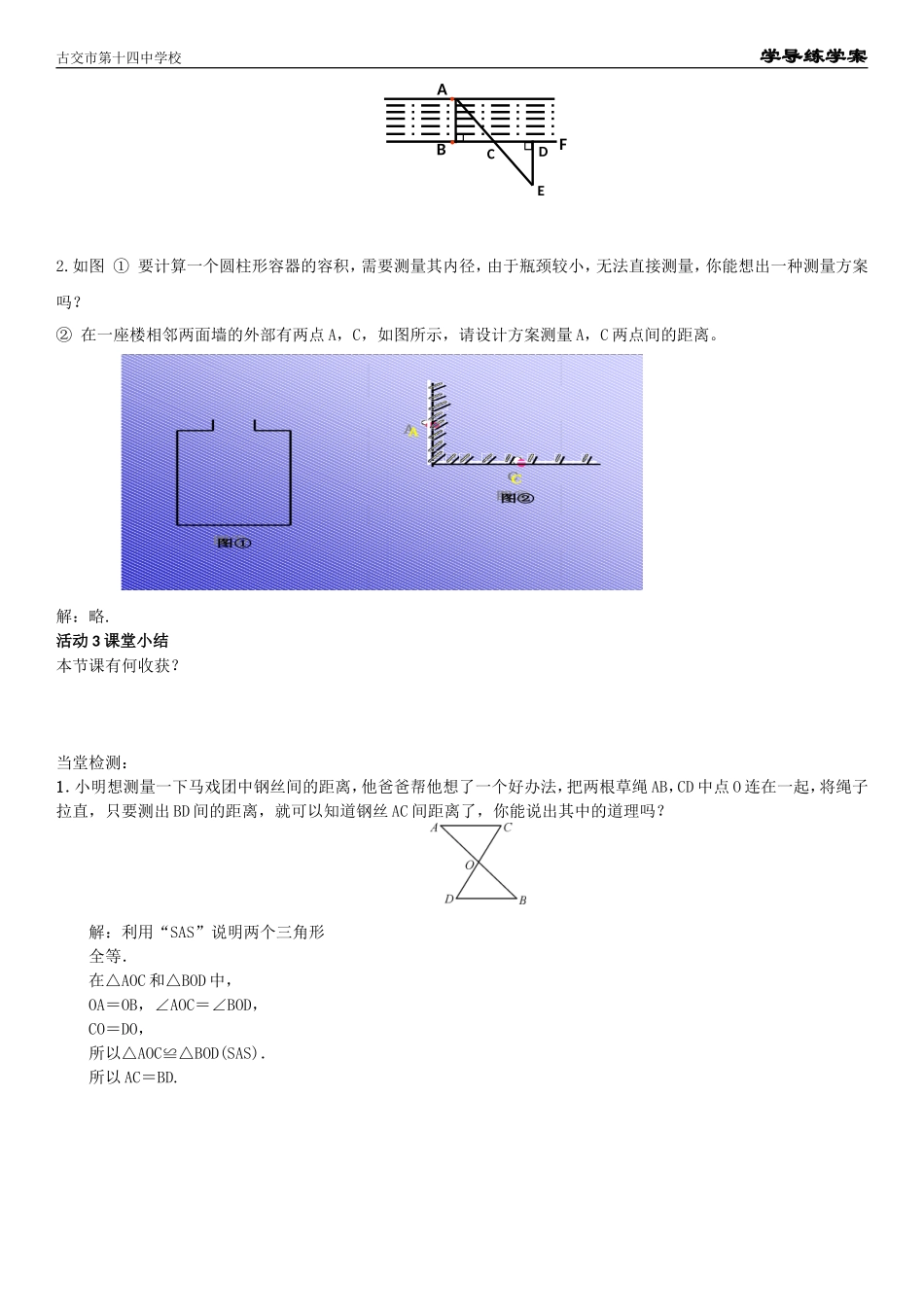
古交市第十四中学校学导练学案4.5利用三角形全等测距离1.能利用三角形的全等解决实际问题,体会数学与实际生活的联系.2.能在解决问题的过程中进行有条理的思考和表述.自学指导阅读课本P108~109,完成下列问题.知识探究1.全等三角形的性质及判定条件是什么?解:略.2.在下列各图中,以最快的速度画出一个三角形,使它与△ABC全等.题如下:解:略.自学反馈1.如图,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示电线杆,BC表示塔松的影长,B′C′表示电线杆的影长,且BC=B′C′,已知电线杆高3m,则塔松高(B)A.大于3mB.等于3mC.小于3mD.和影子的长相同活动1小组讨论例小明在上周末游览风景区时,看到了一个美的池塘,他想知道最远两点A、B之间的距离,但是他没有船,不能直接去测。手里只有一根绳子和一把尺子,他怎样才能测出A、B之间的距离呢?把你的设计方案在图上画出来,并与你的同伴交流你的方案,看看谁是方案更便捷.解:略.活动2跟踪训练1.如图要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长。判定△EDC≌△ABC的理由是(B)A.SSSB.ASAC.AASD.SASAB古交市第十四中学校学导练学案2.如图①要计算一个圆柱形容器的容积,需要测量其内径,由于瓶颈较小,无法直接测量,你能想出一种测量方案吗?②在一座楼相邻两面墙的外部有两点A,C,如图所示,请设计方案测量A,C两点间的距离。解:略.活动3课堂小结本节课有何收获?当堂检测:1.小明想测量一下马戏团中钢丝间的距离,他爸爸帮他想了一个好办法,把两根草绳AB,CD中点O连在一起,将绳子拉直,只要测出BD间的距离,就可以知道钢丝AC间距离了,你能说出其中的道理吗?解:利用“SAS”说明两个三角形全等.在△AOC和△BOD中,OA=OB,∠AOC=∠BOD,CO=DO,所以△AOC≌△BOD(SAS).所以AC=BD.BA●●DCEF