1.1.2平面上的伸缩变换VIP免费

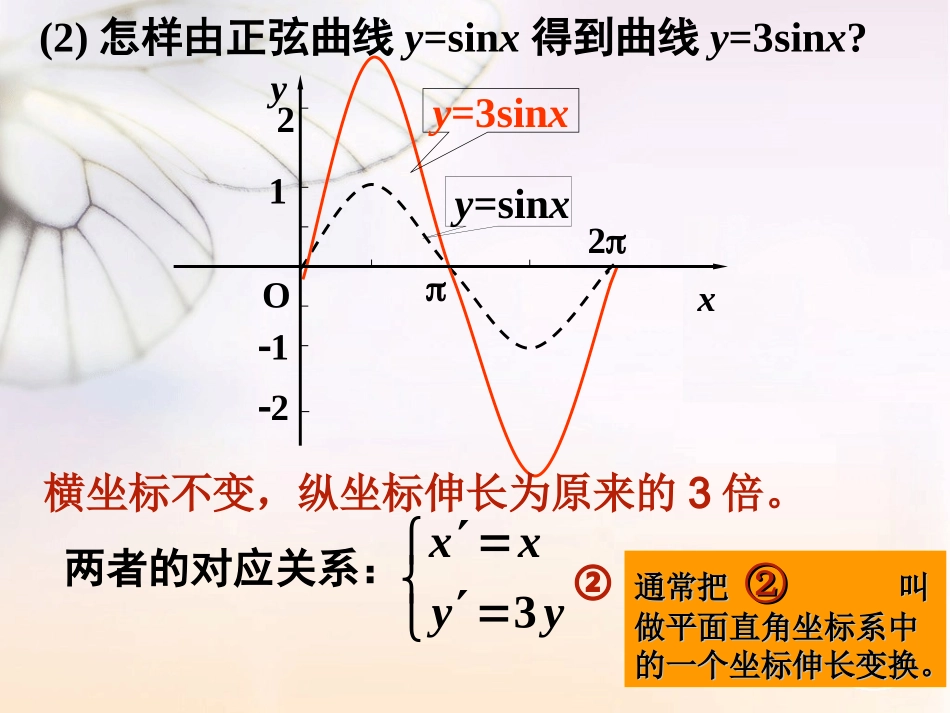
选修4-4坐标系与参数方程1.1.2直角坐标系中------的伸缩变换葫芦岛市第二高级中学迟超xyO2113y=sin2xy=sinx(1)怎样由正弦曲线y=sinx得到曲线y=sin2x?伸缩前点的坐标：(x,y)伸缩后点的坐标：(x′,y′)两者的对应关系：纵坐标不变,横坐标缩短为原来的1/2。12xxyy①通常把通常把叫做平面直叫做平面直角坐标系中的角坐标系中的一个坐标压缩一个坐标压缩变换。变换。①复习回顾y=3sinxy=sinxxyO21221(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?两者的对应关系：横坐标不变，纵坐标伸长为原来的3倍。3xxyy②通常把通常把②②叫叫做平面直角坐标系中做平面直角坐标系中的一个坐标伸长变换。的一个坐标伸长变换。(3)怎样由正弦曲线y=sinx得到曲y=3sin2x?写出其坐标变换.xyO211xx′′==xxyy′′=3=3yy123通常把叫通常把叫做平面直角坐标系做平面直角坐标系中的一个坐标伸缩中的一个坐标伸缩变换。变换。③xyO21134y=sinxy=sinxy=sin2x24xyO12-12y=2sinxy=sinx-2y=sinx？1212平面直角坐标系中的圆锥曲线的伸缩变换思考：（1）已知圆的方程为，在圆上任取一点保持横坐标不变纵坐标变为原来的，则曲线方程变为224xy(,)pxy12224xy————————2214xy224xy2214xyx02-22-2y坐标对应关系为：12xxyy上述的变换中：设P(x,y)是平面直角坐标系中圆上任意一点，保持横坐标不变，将纵坐标y缩为原来，得到点,pxy,,,(,)(,)pxypxy（2）若纵坐标不变，横坐标变为原来的3倍，则曲线变为224xy————x02-22-2y2249xy224xy2249xy在圆上任取一点P（x,y），保持纵坐标y不变，将横坐标伸长为原来的3倍，就得到椭圆。3xxyy设点P（x,y）经变换得到点为,pxy2249xy（3）若横坐标变为原来的3倍，纵坐标变为原来的倍，则曲线变为12224xy————x02-22-2y224xy22136xy22136xy在圆上任取一点P(x,y)，保持横坐标不变，将纵坐标y缩为原来的，在此基础上，将横坐标变为原来的3倍，就得到椭圆设点P（x,y）经变换得到点为312xxyy22136xy,pxy定义：设P(x,y)是平面直角坐标系中任意一点，在变换'(0):'(0)xxyy的作用下，点P(x,y)对应称为平面直角坐标系中的伸缩变换。4注（1）（2）把图形看成点的运动轨迹，平面图形的伸缩变换可以用坐标伸缩变换得到；（3）在伸缩变换下，平面直角坐标系不变，在同一直角坐标系下进行伸缩变换。0,0,pxy例1：在直角坐标系中，求下列方程所对应的图形经过伸缩变换后的图形。（1）2x+3y=0;(2)x2+y2=1213xxyy解：由伸缩变换代入2x+3y=01213xxyy得得x+y=023xxyy22代入x+y=1得2249xy+=11222133xxxxyyyy由伸缩变换得由上所述可以发现，在伸缩变换下，直线仍由上所述可以发现，在伸缩变换下，直线仍然变成直线，而圆可以变成椭圆。然变成直线，而圆可以变成椭圆。思考：思考：在伸缩变换下，椭圆是否可以变成圆？抛物线、在伸缩变换下，椭圆是否可以变成圆？抛物线、双曲线变成什么曲线？双曲线变成什么曲线？结论分析：结论分析：例2.在同一直角坐标系下，求满足下列图形的伸缩变换：曲线4x2+9y2=36变为曲线0xxyy1解：设伸缩变换，22代入x+y=1得22221xy224936xy又1312则1312xxyy得221xy例3.在同一直角坐标系下经过伸缩变换后，曲线C变为，求曲线C的方程并画出图形。3xxyy2299xy22得9x-9y=922即x-y=122x-9y=93xxyy解：将代入课堂练习1将曲线伸缩变换为122yx的伸缩变换公式为()2131.D3121.C23.B32.Ayyxxyyxxyyxxyyxx19422yxA;025yx122yx2、在平面直角坐标系中，求下列方程所对应的图形经过伸缩变换后...