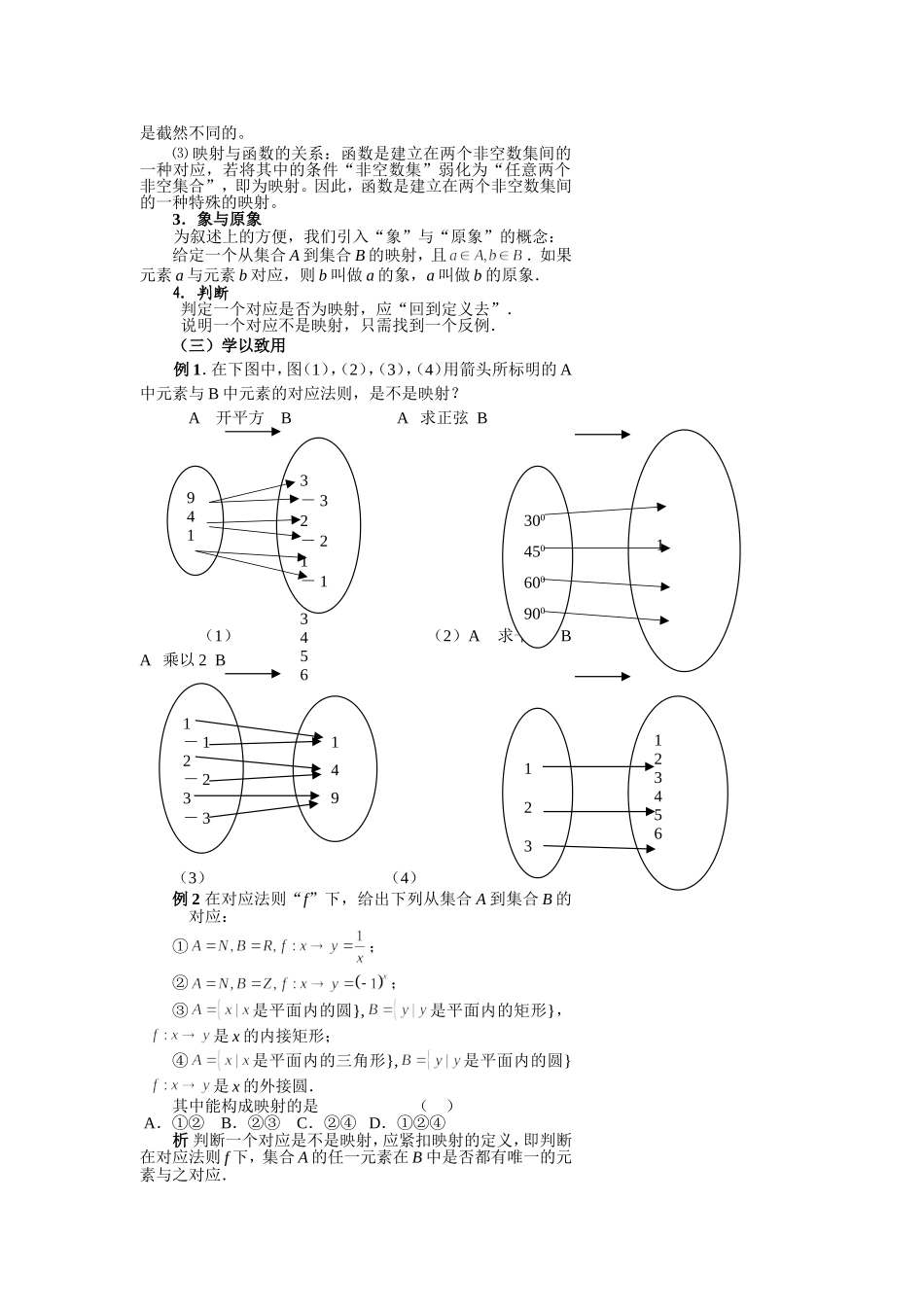
第13课映射的概念一.教学目标1.知识与技能:了解映射的概念及表示方法;2.过程与方法(1)通过实例,归纳共性,抽象出映射的概念;(2)会利用映射的概念来判断“对应关系”是否是映射.3.情态与价值通过本节课的学习,进一步弄清特殊与一般的辨证关系,理解和领会集合与对应思想.二.教学重点:映射的概念教学难点:利用映射的概念进行判断三.学法与教学用具1.学法:通过丰富的实例,学生进行交流讨论和概括;从而完成本节课的教学目标;2.教学用具:多媒体.四.教学思路(一)创设情景1.复习初中常见的对应关系①对于任何一个实数,数轴上都有唯一的点和它对应;②对于坐标平面内任何一个点A,都有唯一的有序实数对()和它对应;③对于任意一个三角形,都有唯一确定的面积和它对应;④某影院的某场电影的每一张电影票有唯一确定的座位与它对应;2.回顾函数的概念.设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一的元素和它对应,那么就称f:A→B为从集合A到集合B的一个函数(function).记作:y=f(x),x∈A.3.归纳以上对应的共同特征(二)探求新知1.映射的概念一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则,使对于集合A中的任意一个元素,在集合B中都有惟一确定的元素与之对应,那么这样的单值对应就称为从集合A到集合B的一个映射(mapping).记作“:A→B”2.对定义的理解⑴理解映射的概念,应紧紧抓住映射的两个特性:①任意性:集合A的任何元素在B中都有元素与之对应;②唯一性:集合A的任何元素在B中只有唯一的元素与之对应,即允许“多对一”,但不允许“一对多”.⑵集合A、B有先后顺序,A到B的映射与B到A的映射是截然不同的。⑶映射与函数的关系:函数是建立在两个非空数集间的一种对应,若将其中的条件“非空数集”弱化为“任意两个非空集合”,即为映射。因此,函数是建立在两个非空数集间的一种特殊的映射。3.象与原象为叙述上的方便,我们引入“象”与“原象”的概念:给定一个从集合A到集合B的映射,且.如果元素a与元素b对应,则b叫做a的象,a叫做b的原象.4.判断判定一个对应是否为映射,应“回到定义去”.说明一个对应不是映射,只需找到一个反例.(三)学以致用例1.在下图中,图(1),(2),(3),(4)用箭头所标明的A中元素与B中元素的对应法则,是不是映射?A开平方BA求正弦B(1)(2)A求平方BA乘以2B(3)(4)例2在对应法则“f”下,给出下列从集合A到集合B的对应:①;②;③是平面内的圆},是平面内的矩形},是x的内接矩形;④是平面内的三角形},是平面内的圆}是x的外接圆.其中能构成映射的是()A.①②B.②③C.②④D.①②④析判断一个对应是不是映射,应紧扣映射的定义,即判断在对应法则f下,集合A的任一元素在B中是否都有唯一的元素与之对应.9413-32-21-1345630045060090011-12-23-3123123456149解①中元素“0”在B中没有元素与之对应,不满足“任意性”,在③中,因为圆的内接矩形有无数个,不满足“唯一性”.所以①,③均不构成映射.在②中,当x为偶数时,与1对应;当x为奇数时,与-1对应。而1,,即A中任一元素在B中都有唯一的元素与之对应.在④中,因为任一三角形都有唯一的外接圆,所以②,④能构成映射.正确答案是C.评⑴在课本中,已规定0是自然数,忽视了这一点,将误认为对应①是映射;⑵在映射中,A、B的地位是不对等的,它并不要求B中元素在A中均有元素与之对应,或有也未必唯一.一般地,若A中元素的象的集合为C,则.如②中除1,-1以外的任何元素在A中均无元素与之对应,④中任一圆的内接三角形都有无数个,不能因此而误认为②,④不构成映射.思考:对于④,对应是的内接三角形是映射吗?例3设集合,试问:从集合A到B可以建立多少个不同的映射?析根据映射的定义,a,b在B中的象共有以下四种可能:评要将符合映射条件的各种对应都考虑到,不能遗漏.例4.若,,对应法.画图说明A到B的对应是映射,并写出与B中元素1对应的A中元素的集合.析首先应化简集合A并用列举法表示出来,其次,应准确理解“f”的意义,图示出各元...