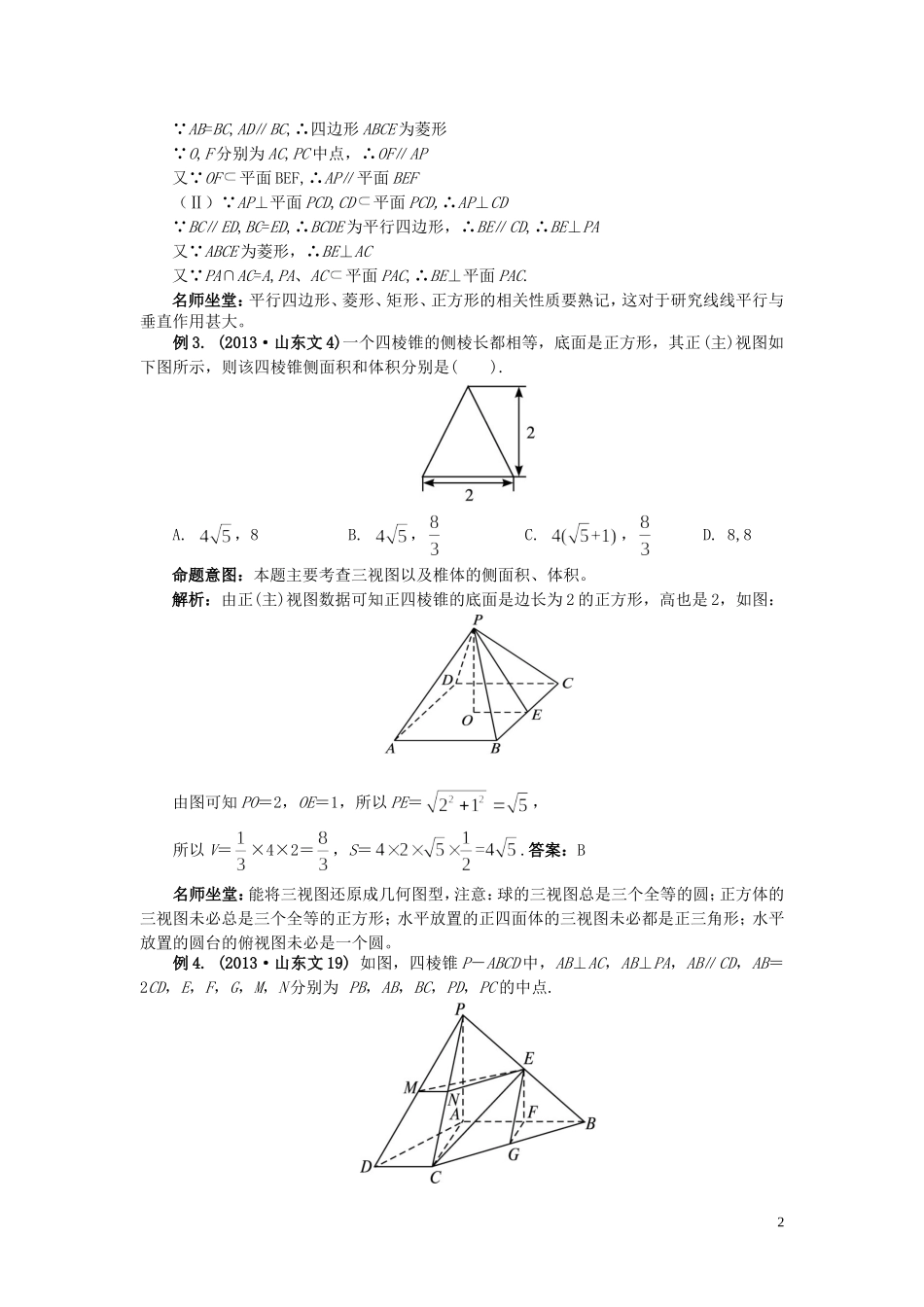
热点八空间几何【考点精要】考点一.棱锥、棱台中的高、斜高。在正棱锥、棱台中利用几个直角三角形(高、斜高以及底面边心距组成的直角三角形,高、侧棱与底面外接圆半径组成一个直角三角形等)进行相关的计算。(1)高、斜高、底面边心距组成的直角三角形;(2)侧棱、斜高、底面棱长的一半组成的直角三角形;(3)底面上的边心距、底面外接圆半径、底面棱长的一半组成的直角三角形.(4)高、侧棱、底面外接圆半径组成的直角三角形.进一步关注的是:侧棱与底面所成角、侧面与底面所成二面角的平面角都体现在这些直角三角形中.考点二.斜二测画法的相关计算。重点考查直观图的顶点与其他关键点,计算时尽量把顶点或其他关键点放在轴上或与轴平行的直线上。考点三.三视图及相关面积、体积的计算。注意掌握三视图之间的规律:正俯长相同、正侧高平齐,俯侧宽相同。考点四.柱体、锥体、台体的侧面积、表面积、体积的运算,简单组合体的体积及面积的计算。注意运用割补法、等体积转化法求解相关体积。考点五.空间中点、线、面的位置关系以及直线、平面平行的判定与性质。近几年来加强了线面之间的距离、异面直线间的夹角、线面平行、线面垂直、面面平行、面面垂直、线线垂直、线面角的考查。考点六.运用坐标法求空间中两点之间的距离以及点关于平面对称点的坐标。巧点妙拨1.垂直和平行涉及题目的解决方法须熟练掌握两类相互转化关系:(1)平行转化:线线平行线面平行面面平行(2)垂直转化:线线垂直线面垂直面面垂直每一垂直或平行的判定就是从某一垂直或平行开始转向另一垂直或平行最终达到目的.2.求异面直线的距离,有时较难作出它们的公垂线,故通常采用化归思想,转化为求线面距、面面距、或由最值法求得.【典题对应】例1.(2014·山东文13)一个六棱锥的体积为,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为。命题意图:几何体的侧面积。解析:设六棱锥的高为h,斜高为h′,则由体积∴侧面积为.答案:12.名师坐堂:几何体的体积的求解时要充分考虑几何体的类型,把握好底和高。例2.(2014·山东文18)如图,四棱锥中,分别为线段的中点.(I)求证:;(II)求证:.命题意图:本题考查线面平行,线面垂直。解析:(Ⅰ)连接AC交BE于点O,连接OF,不妨设AB=BC=1,则AD=21AFCDBPE AB=BC,AD∥BC,∴四边形ABCE为菱形 O,F分别为AC,PC中点,∴OF∥AP又 OF平面BEF,∴AP∥平面BEF(Ⅱ) AP⊥平面PCD,CD平面PCD,∴AP⊥CD BC∥ED,BC=ED,∴BCDE为平行四边形,∴BE∥CD,∴BE⊥PA又 ABCE为菱形,∴BE⊥AC又 PA∩AC=A,PA、AC平面PAC,∴BE⊥平面PAC.名师坐堂:平行四边形、菱形、矩形、正方形的相关性质要熟记,这对于研究线线平行与垂直作用甚大。例3.(2013·山东文4)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如下图所示,则该四棱锥侧面积和体积分别是().A.,8B.,C.,D.8,8命题意图:本题主要考查三视图以及椎体的侧面积、体积。解析:由正(主)视图数据可知正四棱锥的底面是边长为2的正方形,高也是2,如图:由图可知PO=2,OE=1,所以PE=,所以V=×4×2=,S=.答案:B名师坐堂:能将三视图还原成几何图型,注意:球的三视图总是三个全等的圆;正方体的三视图未必总是三个全等的正方形;水平放置的正四面体的三视图未必都是正三角形;水平放置的圆台的俯视图未必是一个圆。例4.(2013·山东文19)如图,四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.2(1)求证:CE∥平面PAD;(2)求证:平面EFG⊥平面EMN.命题意图:本题主要考查几何体中的线面平行、面面垂直,考查学生对线面平行、线面垂直、面面垂直、面面平行等的性质定理与判定定理的区别与应用。(1)证法一:取PA的中点H,连接EH,DH.因为E为PB的中点,所以EH∥AB,EH=.又AB∥CD,CD=,所以EH∥CD,EH=CD.因此四边形DCEH是平行四边形,所以CE∥DH.又DH平面PAD,CE平面PAD,因此CE∥平面PAD.证法二:连接CF.因为F为AB的中点,所以AF=.又CD=,所以AF=CD.又AF∥CD,所以四边形AFCD为平行四边形.因此CF∥AD.又CF平面PAD,所以CF∥平面PAD.因为E,F...