8.3平面向量的分解定理VIP免费

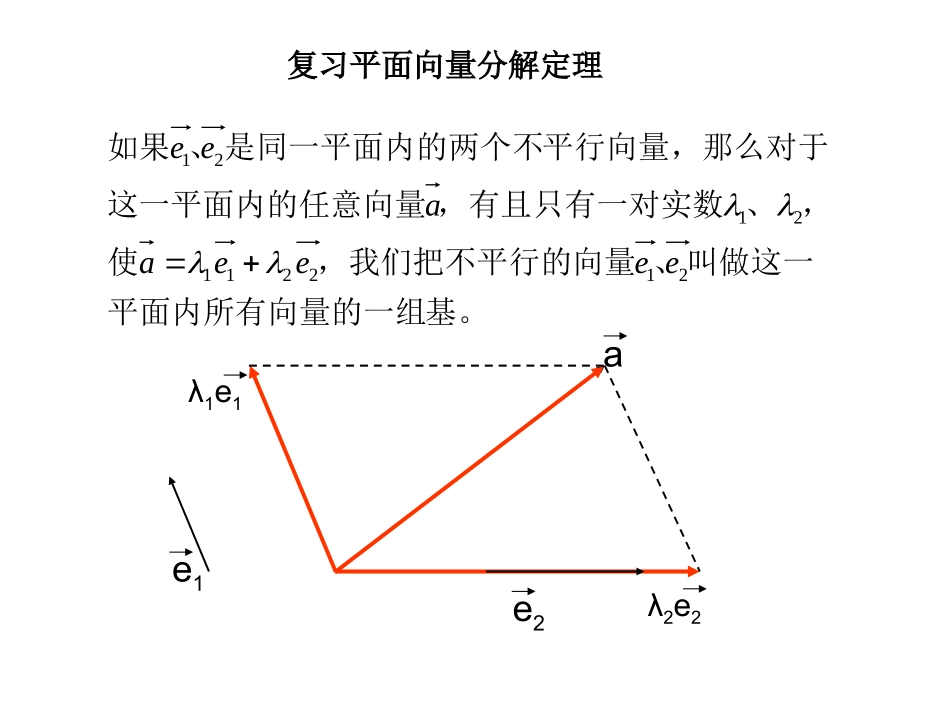
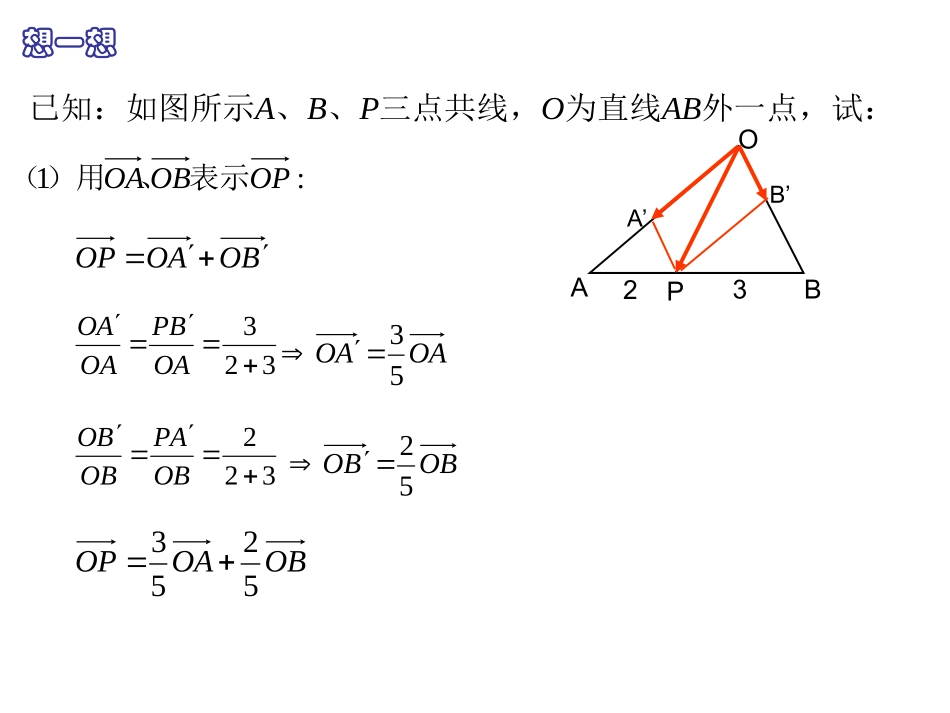
三点共线问题的一个重要结论及应用上海市闸北第八中学杨欣e1e2aλ1e1λ2e2复习平面向量分解定理基。平面内所有向量的一组叫做这一、，我们把不平行的向量使，、，有且只有一对实数这一平面内的任意向量平行向量，那么对于是同一平面内的两个不、如果2122112121eeeeaaeeOAPB23A’B’:1OPOBOA表示、）用（OBOAOP5253想一想323OABPOAAO322OBAPOBBOOAAO53OBBO52BOAOOP外一点，试：为直线三点共线，、、已知：如图所示ABOPBAOAPB23P’B’外一点，试：为直线三点共线，、、已知：如图所示ABOPBA:2OAOPOB表示、）用（POBOOA想一想32PBAPOBAPOBBOOBBO32332OPBAOPPOOPPO35OPOBOA3532OPOBOAOBOAOP353252531解得）中亦可由（OAPB23P’A’想一想外一点，试：为直线三点共线，、、已知：如图所示ABOPBA:3OBOPOA表示、）用（OPOAOB252323APBPOAPBOAAOOAAO23223OPABOPPOOPPO25POAOOBOPOAOBOBOAOP252352531解得）中亦可由（OAPBnmA’B’mn问题1观察三个式子的系数有何共同特点？由此猜想得到什么结论？.1,外一点）为直线（其中三点共线，则有、、若猜想：ABOnmOBnOAmOPPBA)1(PBAPPBA三点共线，可设、、证明：由),(OPOBOAOP则有,)1(OBOAOP推出,111OBOAOP推出,OBnOAmOP即有.,1,1,11mnnmnm其中问题2猜想所得命题的逆命题是否成立？.,1,外一点）为直线（三点共线、、则其中若逆命题：ABOPBAnmOBnOAmOP,1,nmOBnOAmOP其中证明：由OBnOAnOP)1(可得)OAOBnOAOP（则有.三点共线、、，所以即PBAABnAP【结论】，，使得满足、实数唯一一组共线的充要条件是存在、、三点OBnOAmOPnmnmPBA1).外一点为直线（所成的比分且点ABOmnABP则，，边上一点，若是中，在CBCACDDBADABDABC312.12002001}{.2SOCBAOCaOAaOBSnann），则过原点三点共线（该直线不经、、且，，若项和为的前已知等差数列练一练||||3231.3BCABOCOAOBCBAO则，满足，、、、若平面内不共线的四点232100.311nmRnmnOBOQmOAOPQPOBOAPQGOABG），求证：、（，，，且、于点、分别交的线段的重心，过点是三角形如图，点拓展一拓展与提升变式nmANnACAMmABNMACABOBCOABC则，，两点，若、于、的直线分别交直线中点，过是中如图，2拓展与提升拓展二BACxyACyABxAOyxACABABCOcos)0(1232，则若，，，的外心，是已知43拓展与提升D拓展与提升变式BACACyABxAOyxACABABCOcos1343，则若，，，的垂心，是已知94D【小结】1.探究了平面向量中三点共线问题的一个重要结论。2.运用结论解决了平面几何和向量中的几类求值问题。的值是取最大值时，，当上移动时，若在线段，当点，使到，延长，，中，如图ADACAEABEBDBADCBBACACABABC6084思考23变式的最大值是则，上移动时，若在线段，当点使，到，延长，，中，如图tACABAEADEBDBADCBBACACABABC60843332的函数解析式关于，写出，，若、分别交于点、的直线与线段中，已知过点在平行四边形xyOByONOAxOMNMOBOACOABCxxy1思考