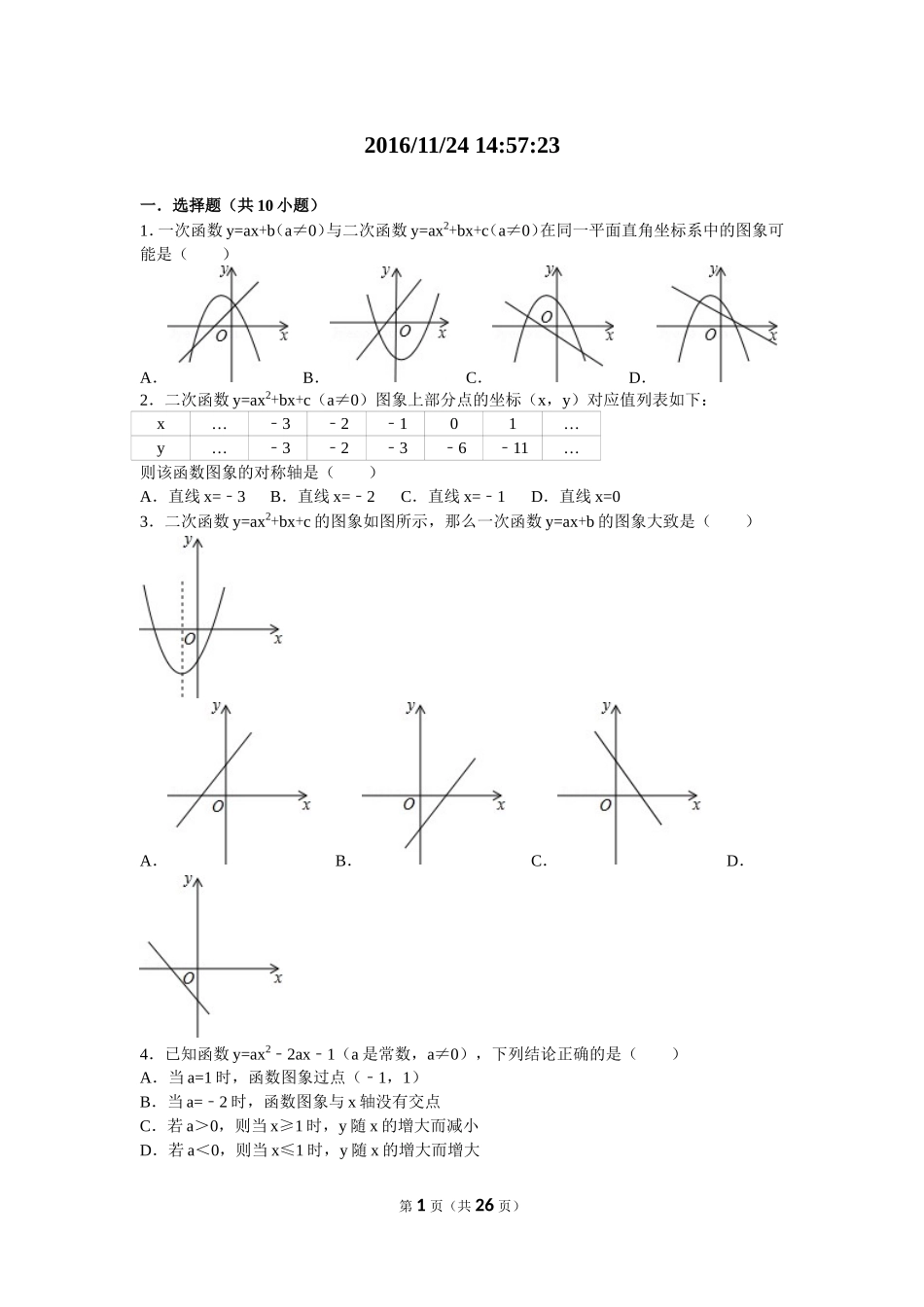
2016/11/2414:57:23一.选择题(共10小题)1.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.2.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:x…3﹣2﹣1﹣01…y…3﹣2﹣3﹣6﹣11﹣…则该函数图象的对称轴是()A.直线x=3﹣B.直线x=2﹣C.直线x=1﹣D.直线x=03.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是()A.B.C.D.4.已知函数y=ax22ax1﹣﹣(a是常数,a≠0),下列结论正确的是()A.当a=1时,函数图象过点(﹣1,1)B.当a=2﹣时,函数图象与x轴没有交点C.若a>0,则当x≥1时,y随x的增大而减小D.若a<0,则当x≤1时,y随x的增大而增大第1页(共26页)5.如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:abc①>04a②+2b+c>04acb③﹣2<8a④<a<b⑤>c.其中含所有正确结论的选项是()A.①③B.①③④C.②④⑤D.①③④⑤6.抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是()A.4B.6C.8D.107.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:ab①﹣+c>0;3a②+b=0;b③2=4a(cn﹣);④一元二次方程ax2+bx+c=n1﹣有两个不相等的实数根.其中正确结论的个数是()A.1B.2C.3D.48.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣,y2)、点C(,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x5﹣)=3﹣的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有()第2页(共26页)A.2个B.3个C.4个D.5个9.点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=x﹣2+2x+c的图象上,则y1,y2,y3的大小关系是()A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y310.二次函数y=﹣(x1﹣)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为()A.B.2C.D.二.选择题(共10小题)11.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=x﹣2+6x上一点,且在x轴上方,则△BCD面积的最大值为.12.二次函数y=x22x3﹣﹣的图象如图所示,若线段AB在x轴上,且AB为2个单位长度,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为.13.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b2c﹣|,Q=|2ab﹣|﹣|3b+2c|,则P,Q的大小关系是.第3页(共26页)14.如图,抛物线y=x﹣2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为.15.a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x22ax﹣+3的图象上,则b、c的大小关系是bc(用“>”或“<”号填空)16.如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=2﹣,则m的值为.17.已知二次函数y=x2+(m1﹣)x+1,当x>1时,y随x的增大而增大,则m的取值范围是.18.抛物线y=x2x﹣+p与x轴相交,其中一个交点坐标是(p,0).那么该抛物线的顶点坐标是.19.如图,在平面直角坐标系中,抛物线y=x22x﹣+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为.20.二次函数y=x22x﹣+b的对称轴是直线x=.三.选择题(共6小题)第4页(共26页)21.如图,已知抛物线y=x﹣2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)(1)求m的值及抛物线的顶点坐标.(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.22.已知平面直角坐标系xOy中,抛物线y=ax2﹣(a+1)x与直线y=kx的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P...