高二数学直线和平面垂直 知识精讲 人教版VIP免费

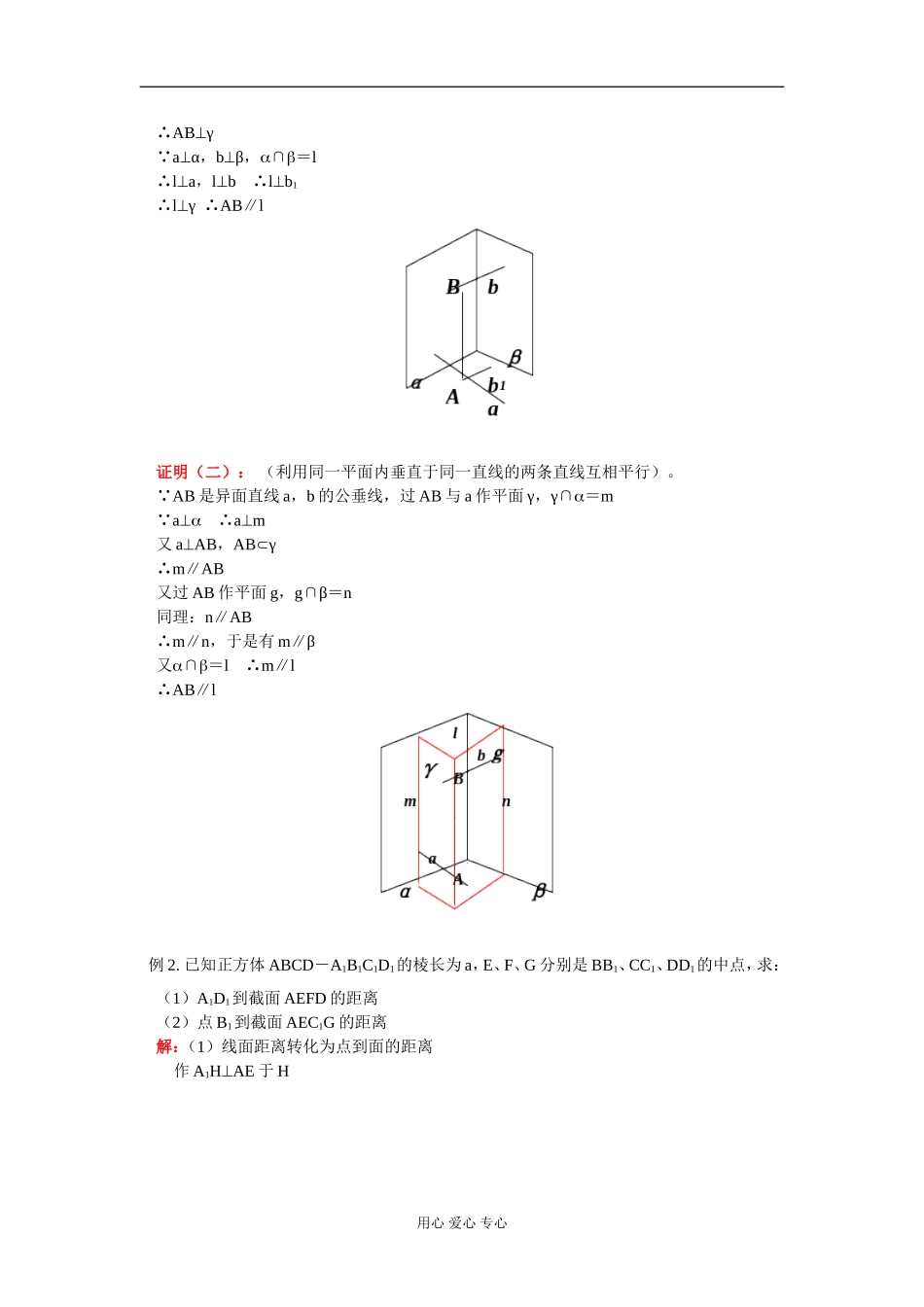
高二数学直线和平面垂直知识精讲人教版一.本周教学内容：直线和平面垂直1.定义：如果一条直线和一个平面内的任何一条直线都垂直就说这条直线和这个平面垂直。2.直线和平面垂直的判定定理⑴判定定理1：如果一条直线和一个平面内两条相交直线都垂直那么这条直线垂直于这个平面。⑵判定定理2：如果两条平行线中的一条垂直于一个平面那么另一条也垂直于这个平面。3.直线和平面垂直的性质定理：如果两条直线同垂直于一个平面，那麽这两条直线平行4.直线和平面的距离：点到平面的距离：从平面外一点引一个平面的垂线，这个点和垂足间的距离，就是点到平面的距离。直线和平面的距离：一条直线和一个平面平行，这条直线上任意一点到平面的距离就是直线和平面的距离。5.直线和平面所成角：一直线垂直于平面，所成的角是直角。一直线平行于平面或在平面内，所成角为0角斜线与平面所成角：斜线与它在这个平面内射影所成的角直线和平面所成角范围：0，二.重点、难点重点：1.直线和平面垂直判定和性质。2.平面外一点到平面距离；直线到平面距离3.直线与平面所成的角难点：1.直线和平面垂直判定和性质定理的应用。2.平面外一点到平面距离，直线到平面距离的求法3.直线与平面所成的角的求法【典型例题】例1.已知：a，b是两条异面直线，a，b，∩＝l，AB是a，b公垂线，交a于A，交b于B求证：AB∥l证明（一）：（利用线面垂直的性质定理）过A作b1∥b，则a，b1可确定一平面γ AB是异面垂线的公垂线，即ABa，ABb∴ABb1用心爱心专心∴ABγ aα，bβ，∩＝l∴la，lb∴lb1∴lγ∴AB∥l证明（二）：（利用同一平面内垂直于同一直线的两条直线互相平行）。 AB是异面直线a，b的公垂线，过AB与a作平面γ，γ∩＝m a∴am又aAB，ABγ∴m∥AB又过AB作平面g，g∩β＝n同理：n∥AB∴m∥n，于是有m∥β又∩＝l∴m∥l∴AB∥l例2.已知正方体ABCD－A1B1C1D1的棱长为a，E、F、G分别是BB1、CC1、DD1的中点，求：（1）A1D1到截面AEFD的距离（2）点B1到截面AEC1G的距离解：（1）线面距离转化为点到面的距离作A1HAE于H用心爱心专心 EF||BC∴EF平面ABB1A1∴EFA1H AE∩EF＝E∴A1H平面AEFD A1D1||平面AEFD∴A1H的长是A1D1到截面AEFD的距离 RtΔA1HA∽RtΔABE AB＝a，BE＝a/2，A1A＝a∴AE＝＝a RTΔA1HA∽RTΔABE∴A1H＝＝＝a（2）点面距离转化为线面距离扩大了选择点的自由连接B1D1、GE∴GE||B1D1 B1D1平面AEC1GEG平面AEC1G∴B1D1||平面AEC1G∴B1D1上任意一点到平面AEC1G的距离都相等连接A1C1、AC1，设A1C1∩B1D1＝O1 A1A平面A1B1C1D1∴A1AB1D1 A1C1、B1D1是正方形A1B1C1D1的对角线∴A1C1B1D1 A1A∩A1C1＝A1∴B1D1平面AA1C1∴EG平面AA1C1 EG平面AEC1G∴平面AA1C1平面AEC1G，交线AC1过O1作O1HAC1于H∴O1H平面AEC1G用心爱心专心由RtΔC1HO1∽RtΔC1A1AA1A＝a，AC1＝a，O1C1＝a∴O1H＝＝＝a∴点B1到截面AEC1G的距离为a。解法（二）：等体积法解连接EG，VB1－C1EG＝VG－B1EC1 D1D||平面BC1∴D1D到平面BC1距离相等∴G到平面BC1距离为a，SΔB1EC1＝a＝ C1G＝C1E∴C1OGE O为GE中点∴OC1＝a，GO＝a∴SΔC1EG＝＝a2∴∴h＝将点到平面的距离转化为直线到平面的距离，这样做的目的是加大了作垂线的自由度。作垂线时利用“两个平面垂直的性质定理”，把从一点向已知平面作垂线的问题转化为找过这个点的已知平面的垂线。确定它们的交线，只需由这点向它们的交线作垂线即可。例3.已知正方体ABCD－A1B1C1D1，E、F分别是AB、C1D1的中点，求：直线AB与平面A1ECF所成的角解：正方体ABCD－A1B1C1D1中E、F分别是AB、C1D1中点∴A1E＝CE＝CF＝FA1A1F∥CE∴A1ECF为棱形∴EF⊥A1C设A1C∩EF＝O，∴O为A1CEF中点 B1E＝B1F∴在△B1EF中，有B1O⊥EF用心爱心专心又EF⊥A1C∴EF⊥平面A1B1C又EF平面A1ECF∴平面A1EFC⊥平面A1B1C在平面A1B1C内作B1H⊥A1C于H，则B1H⊥平面A1ECF A1B1∥AB∴A1B1与平面A1ECF所成角等于AB与平面A1ECF所成角等于∠B1A1H设正方体棱长为1，则A1C＝B1H＝（1*）/＝（A1H＝＝）∴sin∠B1A1H＝∴∠B1A1H＝arcsin即：AB与平...