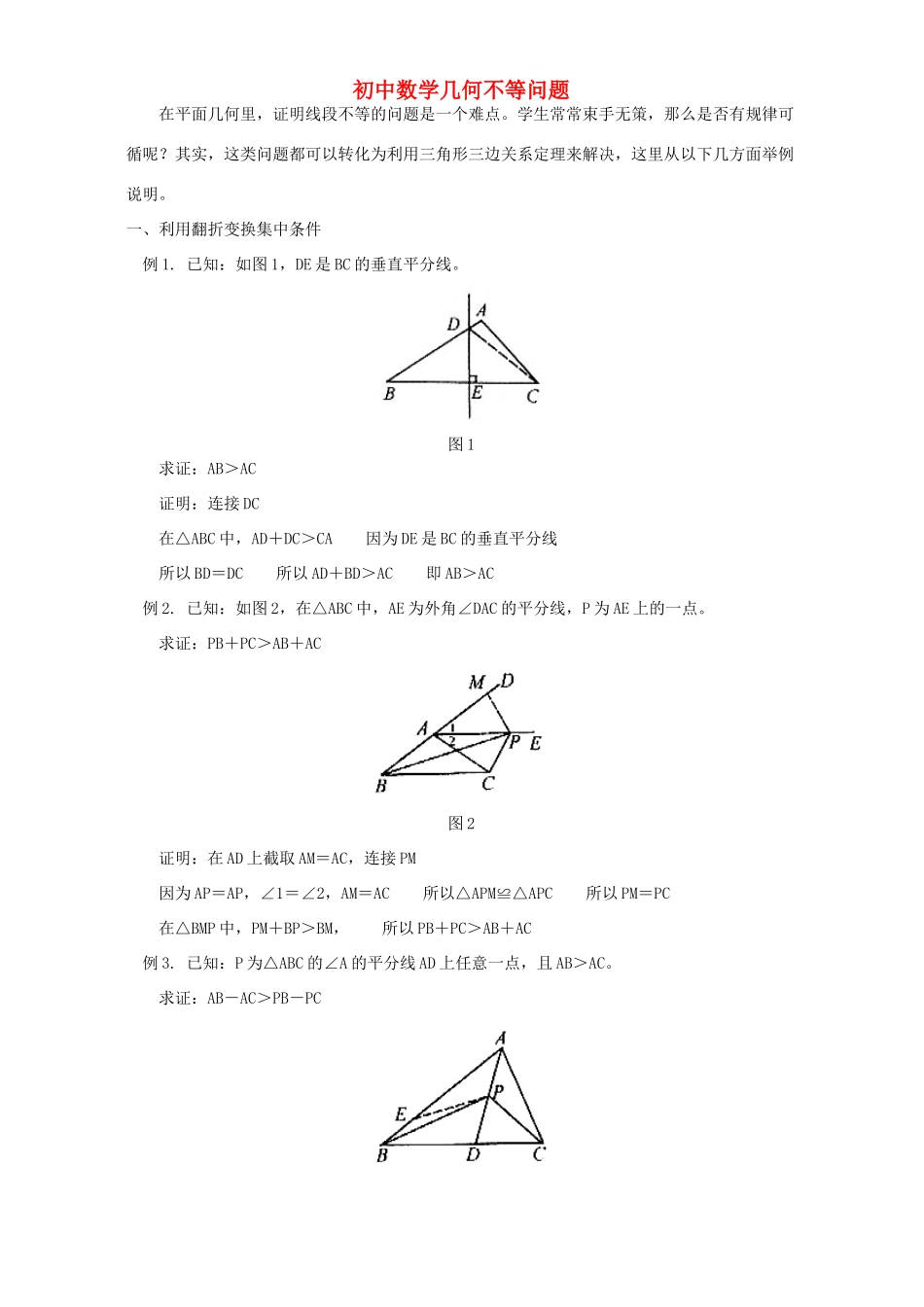
初中数学几何不等问题在平面几何里,证明线段不等的问题是一个难点。学生常常束手无策,那么是否有规律可循呢?其实,这类问题都可以转化为利用三角形三边关系定理来解决,这里从以下几方面举例说明。一、利用翻折变换集中条件例1.已知:如图1,DE是BC的垂直平分线。图1求证:AB>AC证明:连接DC在△ABC中,AD+DC>CA因为DE是BC的垂直平分线所以BD=DC所以AD+BD>AC即AB>AC例2.已知:如图2,在△ABC中,AE为外角∠DAC的平分线,P为AE上的一点。求证:PB+PC>AB+AC图2证明:在AD上截取AM=AC,连接PM因为AP=AP,∠1=∠2,AM=AC所以△APM≌△APC所以PM=PC在△BMP中,PM+BP>BM,所以PB+PC>AB+AC例3.已知:P为△ABC的∠A的平分线AD上任意一点,且AB>AC。求证:AB-AC>PB-PC图3证明:在AB上截取AE=AC,连接EP因为AD平分∠BAC所以∠BAD=∠CAD又因为AE=AC,AP=AP∴△AEP≌△ACP所以PE=PC在△BEP中,BE>BP-PC所以AB-AE>BP-PC即AB-AC>BP-PC二、利用旋转变化集中条件例4.在△ABC中,AD为BC边上的中线求证:2AD<AB+AC图4证明:如图4,延长AD至E使DE=AD,连接BE,易知△EBD≌△ACD,EB=AC在△ABE中,AE<AB+BE,所以2AD<AB+AC例5.已知:如图5,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF求证:BE+CF>EF图5证明:延长ED到G使DG=ED,连接CG、FG则△BED≌△CGD所以CG=BE又DE⊥DF所以FG=EF在△FGC中,所以CG+CF>FG所以BE+CF>EF三、利用全等变换集中条件例6.在⊙O中,C是弧AB的中点,D是弧AC上的任意一点,(与点C不重合),则()图6A.AC+CB=AD+DBB.AC+CB<AD+DBC.AC+CB>AD+DBD.AC+CB与AD+DB的大小关系不确定证明:延长BD至E使DE=AD,连接EC,DC因为弧AC=弧BC所以∠ABC=∠BDC因为∠ADC+∠ABC=180°∠EDC+∠BDC=180°所以∠ADC=∠EDC又因为AD=DE,DC=DC所以△CAD≌△EDC即AC=EC在△BEC中,BC+EC>BE所以BC+AC>BD+AD故选C。由上几例可以看出,有关边不等的问题的一般规律是:通过某些变换,使要证明的边聚集在同一个三角形内,然后再利用三边关系定理进行论证。