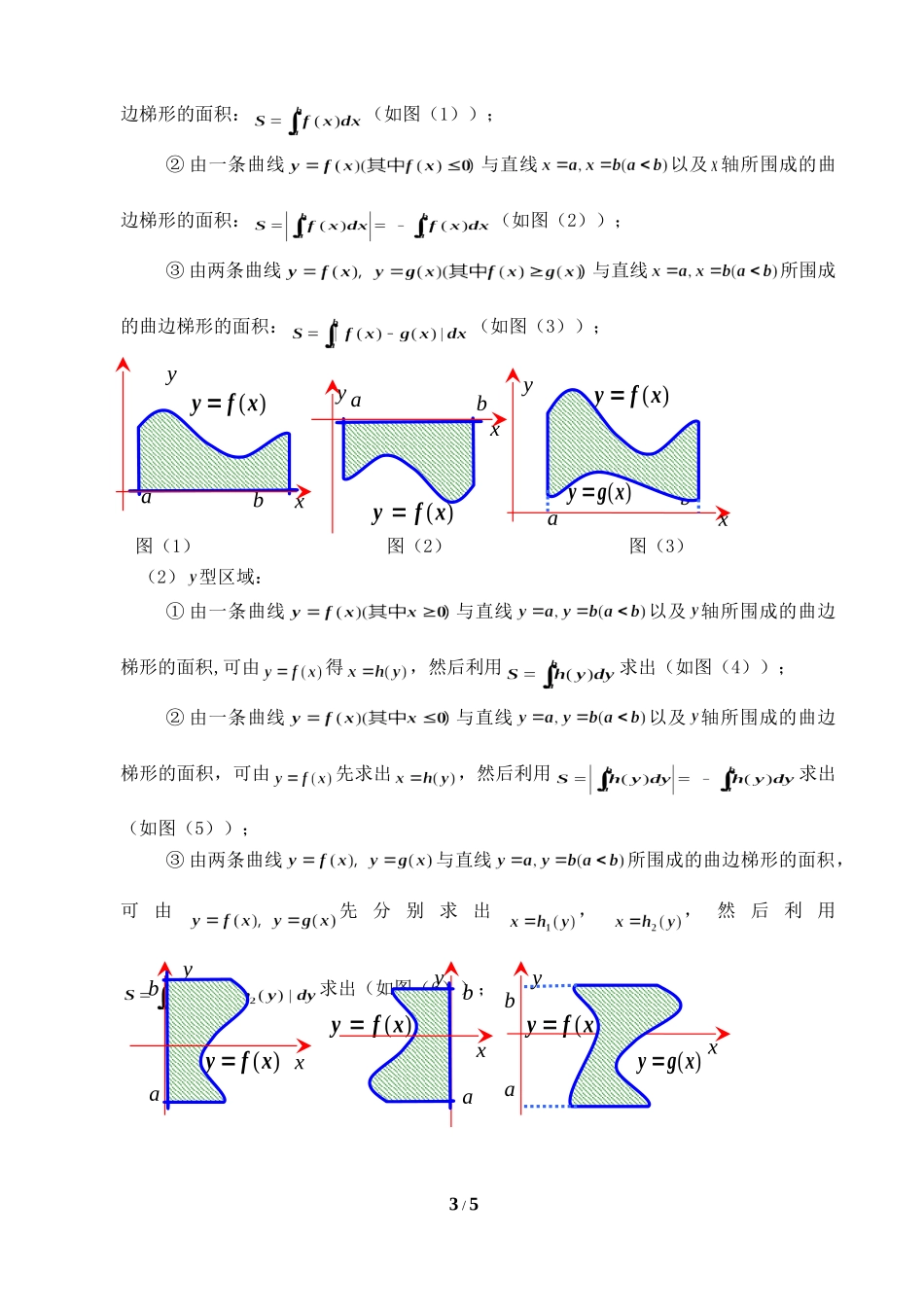
定积分的简单应用教学目标:1、进一步让学生深刻体会“分割、以直代曲、求和、逼近”求曲边梯形的思想方法;2、让学生深刻理解定积分的几何意义以及微积分的基本定理;3、初步掌握利用定积分求曲边梯形的几种常见题型及方法,以及利用定积分求一些简单的旋转体的体积;4、体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。教学重点:几种曲边梯形面积的求法。教学难点:定积分求体积以及在物理中应用。教学过程:一、问题情境1、求曲边梯形的思想方法是什么?2、定积分的几何意义是什么?3、微积分基本定理是什么?二、数学应用(一)利用定积分求平面图形的面积例1、求曲线与直线轴所围成的图形面积。答案:变式引申:1、求直线与抛物线所围成的图形面积。答案:2、求由抛物线及其在点M(0,-3)和N(3,0)处的两条切线所围成的图形的面积。略解:,切线方程分别为、,则所求图形的面积为1/5xyoy=-x2+4x-33、求曲线与曲线以及轴所围成的图形面积。略解:所求图形的面积为4、在曲线上的某点A处作一切线使之与曲线以及轴所围成的面积为.试求切点A的坐标以及切线方程.略解:如图由题可设切点坐标为,则切线方程为,切线与轴的交点坐标为,则由题可知有,所以切点坐标与切线方程分别为总结:1、定积分的几何意义是:、轴所围成的图形的面积的代数和,即.因此求一些曲边图形的面积要可以利用定积分的几何意义以及微积分基本定理,但要特别注意图形面积与定积分不一定相等,如函数的图像与轴围成的图形的面积为4,而其定积分为0.2、求曲边梯形面积的方法与步骤:(1)画图,并将图形分割为若干个曲边梯形;(2)对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;(3)确定被积函数;(4)求出各曲边梯形的面积和,即各积分的绝对值的和。3、几种常见的曲边梯形面积的计算方法:(1)型区域:①由一条曲线与直线以及轴所围成的曲2/5xxOy=x2ABC边梯形的面积:(如图(1));②由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(2));③由两条曲线与直线所围成的曲边梯形的面积:(如图(3));图(1)图(2)图(3)(2)型区域:①由一条曲线与直线以及轴所围成的曲边梯形的面积,可由得,然后利用求出(如图(4));②由一条曲线与直线以及轴所围成的曲边梯形的面积,可由先求出,然后利用求出(如图(5));③由两条曲线与直线所围成的曲边梯形的面积,可由先分别求出,,然后利用求出(如图(6));3/5y)(xfy)(xgyabxy)(xfyabxy)(xfyabxy)(xfy)(xgyabxy)(xfyabxy)(xfyabx图(4)图(5)图(6)(二)、定积分求旋转体体积例2:求由曲线所围成的图形绕轴旋转所得旋转体的体积。分析:(1)分割:将旋转体沿轴方向将区间[0,1]进行等分;(2)对区间上的柱体以区间右端点对应的函数值的平方数作为底面圆半径的平方,以作为圆柱的高,以此圆柱体积近似代替曲边圆柱的体积,即;(3)求和;(4)逼近:当分割无限变细时,即趋近于0时,根据定积分的定义其极限即为旋转体的体积。略解:(三)、定积分在物理中应用(1)求变速直线运动的路程例3、A、B两站相距7.2km,一辆电车从A站B开往站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,经ts后,速度为(24-1.2t)m/s,在B点恰好停车,试求(1)A、C间的距离;(2)B、D间的距离;(3)电车从A站到B站所需的时间。分析:作变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即略解:(1)设A到C的时间为t1则1.2t=24,t1=20(s),则AC=4/5(2)设D到B的时间为t21则24-1.2t2=0,t21=20(s),则DB=(3)CD=7200-2240=6720(m),则从C到D的时间为280(s),则所求时间为20+280+20=320(s)(2)、变力沿直线所作的功问题:物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a点移动到x=b点,则变力F(x)所做的功为:例3:如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功(A)A0.18JB0.26JC0.12JD0.28J略解:设,则由题可得,所以做功就是求定积分。五:回顾与小结:...