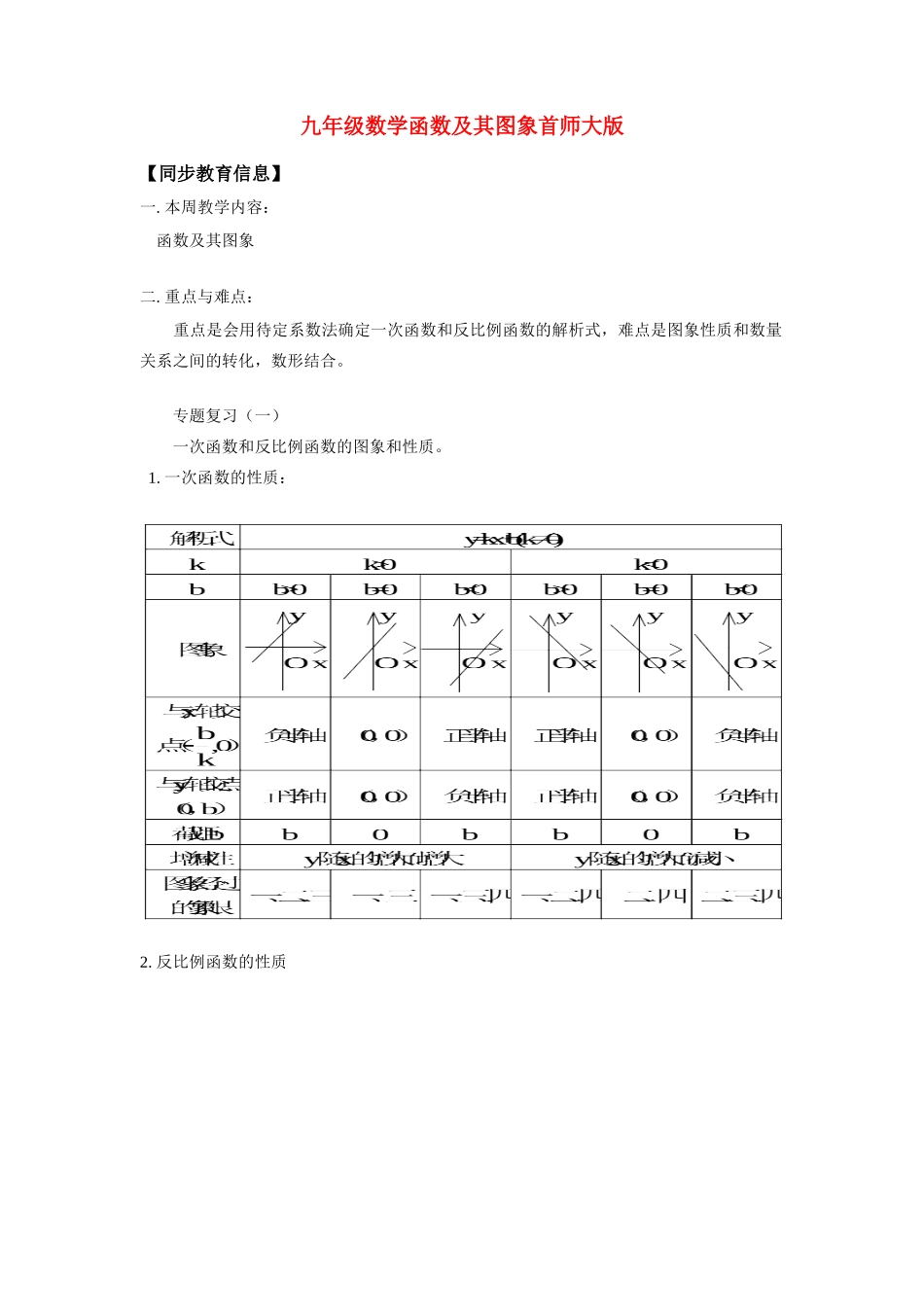
九年级数学函数及其图象首师大版【同步教育信息】一.本周教学内容:函数及其图象二.重点与难点:重点是会用待定系数法确定一次函数和反比例函数的解析式,难点是图象性质和数量关系之间的转化,数形结合。专题复习(一)一次函数和反比例函数的图象和性质。1.一次函数的性质:2.反比例函数的性质3.一次函数与正比例函数:当一次函数y=kx+b(k≠0)中的截距b为0时,即y=kx(k≠0)即为正比例函数,所以正比例函数是一次函数的特殊形式。4.一次函数的图象:一次函数的图象是与坐标轴不平行的一条直线,其中正比例函数的图象,是过原点的直线。一次函数的图象是一条直线,但直线不一定是一次函数的图象。如x=a,y=b分别是与y轴、x轴平行的直线,就不是一次函数的图象。5.一次函数、一次方程和一次不等式的关系:一次函数y=ax+b(k≠0),当函数y的值等于0时,就得到了一元一次方程ax+b=0,此时的自变量x的值就是方程的解,即这个一次函数的图象与x轴的交点的横坐标;当x、y看作是两个变量时,ax-y+b=0即为二元一次方程。一元一次不等式ax+b>0(或ax+b<0)的解集,是当一次函数y=ax+b(k≠0)大于0(或小于0)时,对应的自变量x的值,那么函数图象中在x轴上方(或下方)的所有点的横坐标,即为满足不等式的解集,因为,点在x轴的上方(或下方),意味着它的纵坐标(y的值)大于(或小于)0,而y等于右端的解析式ax+b。当不等号是“≥”或“≤”时,解释同理。6.反比例函数的认识:反比例函数的解析式的三种形式:【例题选讲】例1.A.等边三角形B.只有两边相等的等腰三角形C.直角三角形D.梯形分析:这种题目涉及图形的面积,需要画出草图,发挥数形结合的优势,借助图形帮助思考,其中直线y=-2是过点(0,-2)且与x轴平行的直线,如图,设直线l1:y=3x+2,∴△ABC不是等边三角形,而是只有两边相等的等腰三角形,应选B。例2.已知二元一次方程4x+y=5和x-2y=8(1)把这两个方程改写成关于x的一次函数;(2)在同一坐标系中作出它们的图象;(3)利用图象求出两条直线交点的坐标;并说明方程组的解与两直线交点坐标之间的关系。分析:本题是二元一次方程与一次函数的关系,第(3)问题从形的方面解二元一次方程组,第(4)问是从数量关系上解二元一次方程组,注意,从图上读出的两直线的交点坐标只是估计值,不一定准确,而用数量关系解出的方程组的解才是准确的,第(5)问是从形上去解一元一次不等式。解:(2)如图(3)过交点A分别作x、y轴的垂线,垂足所对应的点的坐标即为交点A的横纵坐标A(-2,3)。的解,从图形上说,l1与l2的交点A(2,-3)既在直线l1上,又在直线l2上;从数量关一对应。(即y值)大于直线l2上的点的纵坐标(即y值)的所有点的横坐标。也就是直线l1上所有在直线l2上方的点的横坐标。以A(2,-3)为分界点即解集为x<2。例3.m在什么范围内取值时,直线y=2x+1-m和直线y=-x-2m-3的交点在第二象限内?分析:先求出交点坐标,根据第二象限内的点的坐标的符号,横坐标小于0,纵坐标大于0,可列不等式求出m的值。解:例4.如图,OB⊥OA于O,以OA为半径画弧交OB于B,OA=2cm,点P是半径OA上的动点;设OP=xcm,阴影部分的面积为ycm2(1)求y与x的函数解析式及自变量x的取值范围;(2)画出此解析式的图象;解:(2)如图,函数的图象是一条以点(2,π-2)和点(0,π)为端点的线段。例5.如果y与z成正比例关系,z与x成反比例关系,问y与x成什么关系?分析:应利用已知的关系写出y与x的关系式。解:由已知y与z成正比例关系,可设y=k1z,其中k1≠0,且k1是常数,又由已知z与x成反比例关系,可设例6.在直角坐标系中,O是原点,点A的坐标是(4,0),点P(x,y)是第一象限内直线x+y=6上的动点,△POA的面积为S(如图)(1)写出S关于x的函数表达式,并求x的取值范围;(2)若把x看作S的函数,求函数的解析式,并求S的取值范围;(3)当S=10时,求点P的位置;(4)在直线x+y=6上求一点P,使△POA是等腰三角形。解:(2)若把x看作S的函数,由S=-2x+12,(4) OA=4,∴当点B的坐标是(2,0)时,PB在△POA的底边OA的垂直平分线上,此时,PO=PA,而点P的横坐标是x=2,代入直线方程x+y...