1.2.1几个常见函数的导数VIP免费

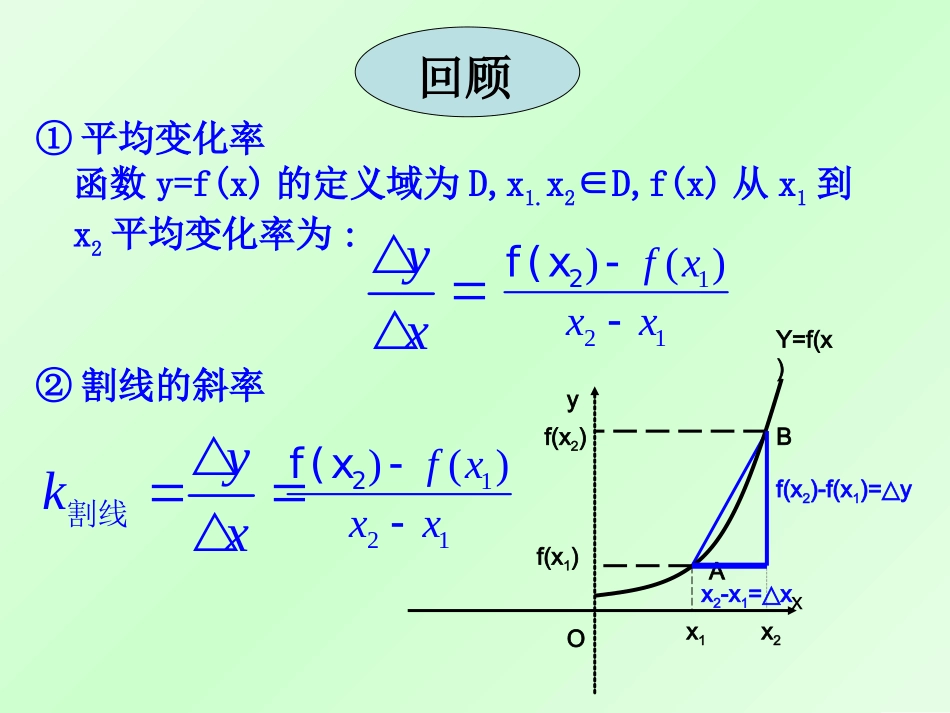
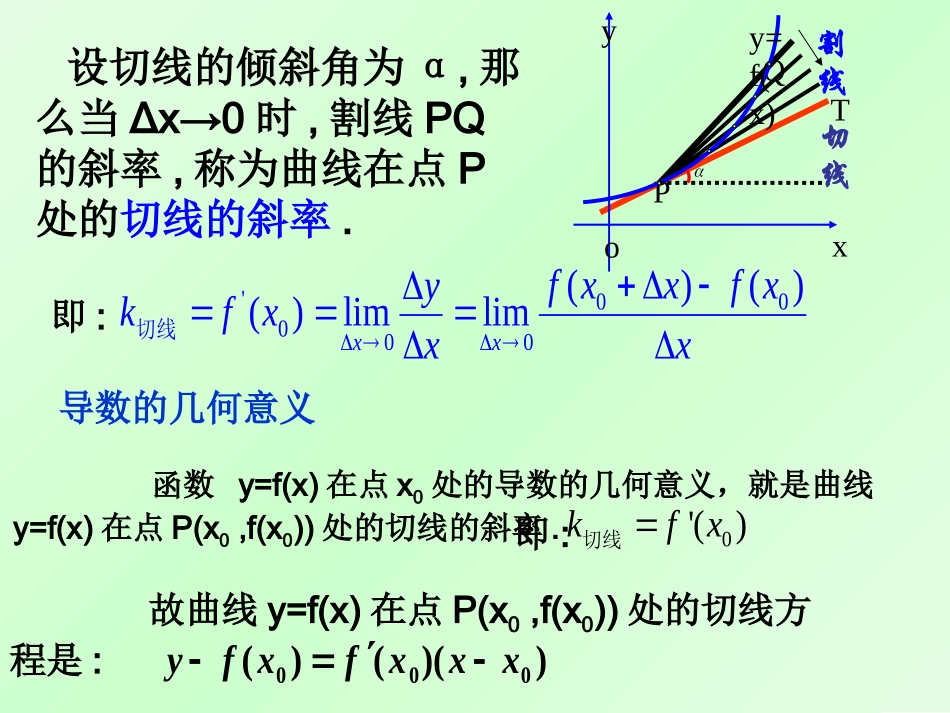
1.2.1几个常用函数的导数回顾①平均变化率yx121)()fxxx2f(x函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2平均变化率为:②割线的斜率OABxyY=f(x)x1x2f(x1)f(x2)x2-x1=x△ykx割线121)()fxxx2f(xf(x2)-f(x1)=y△设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即:'00000()()()limlimxxfxxfxykfxxx切线PQoxyy=f(x)割线切线T导数的几何意义函数y=f(x)在点x0处的导数的几何意义，就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.即:0'()kfx切线故曲线y=f(x)在点P(x0,f(x0))处的切线方程是:))(()(000xxxfxfy2.求函数的导数的方法是:(1)()();yfxxfx求函数的增量(2):()();yfxxfxxx求函数的增量与自变量的增量的比值0(3)()lim.xyyfxx求极限，得导函数说明:上面的方法中把x换成x0即为求函数在点x0处的导数.说明:上面的方法中把x换x0即为求函数在点x0处的导数.3.函数f(x)在点x0处的导数就是导函数在x=x0处的函数值,即.这也是求函数在点x0处的导数的方法之一。)(0xf)(xf0|)()(0xxxfxf函数f(x)在x=x0处求导数反映了函数在点(x0,y0)附近的变化规律;1)|F’(x)|越大,则f(x)在(x0,y0)附近就越“陡”2)|F’(x)|越小,则f(x)在(x0,y0)附近就越“平缓”二、新课——几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.公式1:.0()CC为常数1.函数y=f(x)=c的导数.2.函数y=f(x)=x的导数.'1x思考82页探究1一次函数y=f(x)=kx（k≠0）的导数.kkx'请同学们求下列函数的导数:21(),2(),13(),yfxxyfxxyfxx、、、'1y21'yx'2yx通过以上我们能得到什么结论?4f(x)x,、y=1'2yx'1(x)x(为常数）3.幂函数:例：求下列函数的导数'1(x)x(为常数）4.幂函数:(sin)cos;xxxxsin)(cos4、三角函数：例、求下列函数的导数(1)sin()(2)sin23(3)cos(2)yxyyx6、对数函数：1(log)(01)lnaxaaxa且特别：xx1)(ln5、指数函数：)10(ln)(aaaaaxx且特别：xxee)(3(1)4(2)logxyyx练习：注意:关于是两个不同的函数,例如:axxa和)3)(1(x))(2(3x3ln3x23x1、求下列函数的导数xyytyx2.0log)3(2)2(sin)1((7)2(8)xyye2(),(1)4,.afxxfa、已知且求实数练习:(6)lnyx341(9)yxxvucos)4(xy3)5(1、常函数：2、一次函数：3、幂函数：0Ckkx)(1()xx特别：1x特别：xx2)(221)1(xx4、三角函数：xxxxsin)(cos;cos)(sin5、对数函数：1(log)(01)lnaxaaxa且特别：xx1)(ln6、指数函数：)10(ln)(aaaaaxx且特别：xxee)(